In diesem Abschnitt wird das Tool Inverse Distance Weighting zur Interpolation von Daten in 2D und 3D erläutert. Sie finden diese Funktionen in der Hauptmenüleiste unter Modelling. Zum Format der Eingangsdaten lesen Sie bitte hier nach.
Wenn Sie mehr über die Berechnung erfahren wollen, können wir die Erläuterung des Wikipedia empfehlen: https://en.wikipedia.org/wiki/Inverse_distance_weighting.
Kurz zusammengefasst kann man aber sagen, dass beim Inverse Distance Weighting am Interpolationspunkt ein auf die Summe aller Gewichte normierter gewichteter Mittelwert der Eingabewerte berechnet wird. Das Gewicht, also die Einflussnahme eines einzelnen Eingabewertes auf den Mittelwert am Interpolationspunkt, bemisst sich dabei an seiner Distanz vom Interpolationspunkt - und zwar genau genommen an der reziproken Distanz mit einem vom Nutzer festgelegten Exponenten. Mit Erhöhung oder Erniedrigung des Exponenten (Pow of weighting) steuert der Nutzer, ob die Einflussnahme eines Punktes mit der Distanz rascher oder weniger rasch abnimmt. Zur Verständlichkeit haben wir hier die Formel für die Gewichtsberechnung aus Wikipedia noch einmal eingefügt:
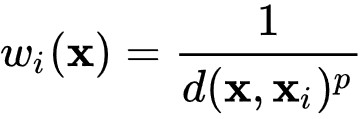
wi = Gewicht eines Eingabewertes i.
x = Standort des Interpolationspunktes.
xi = Standort des Eingabewertes i.
d(x, xi) = Distanz zwischen Interpolationspunkt und Eingabewert i.
p = Exponent, der vom Nutzer eingestellt wird.
Die obige Formel verdeutlicht, dass ein hoher Wert für den Exponenten auch bedeutet, dass ein Eingabewert auch schon bei kürzeren Distanzen seinen Einfluss verliert, weil sein Gewicht sehr klein wird.
Und hier die vollständige Berechnung des Interpolationspunktes:
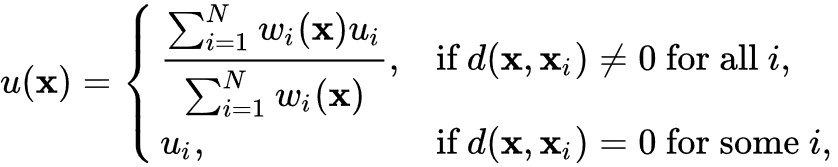
u = Resultat am Interpolationspunkt.
ui = Wert der Eingabe i.
sonst s.o.
Sie können anhand der Formel oben auch sehen, dass an einem Interpolationspunkt, der in sehr geringer Distanz (~0) zum Eingabewert i liegt, der Eingabewert i gesetzt wird und alle anderen Punkte keinerlei Einflussnahme mehr haben.
Neben der Definition des Exponenten, beeinflussen Sie die Berechung durch eine Eingabe in dem Abschnitt max.point number, welche Sie sowohl im 2D- als auch im 3D-IDW Tool vorfinden werden. Wird ein Interpolationspunkt berechnet, werden zunächst alle Distanzen zu den Eingabewerten berechnet und dann nach Distanz aufsteigend sortiert. Nutzen Sie also nicht die gesamte Anzahl der Punkte (Eingabewert = 0), dann werden nur diejenigen Eingabewerte zur Interpolation herangezogen, die am nächsten dran liegen. Geben Sie hier beispielsweise eine 10 ein, dann werden nur die 10 nächsten Punkte vom Interpolationspunkt in die Berechnung eingehen, alle anderen ignoriert. Hier sollten Sie sich jedoch die räumliche Verteilung Ihrer Daten zuvor genauer ansehen, um nicht unplausible Ergebnisse zu produzieren. Dies ist besonders zu beachten, wenn räumlich strukturierte Daten mit stark ungleicher räumlicher Verteilung vorliegen. Die Anzahl der Punkte zu beschränken kann auch sinnvoll sein, wenn Sie mit einem Datensatz >~5000 Punkte reingehen. Dann kann die Berechnung länger dauern und Sie könnten hiermit Berechnungsschritte reduzieren.
Voronoi mit IDW erzeugen:
Wenn Sie sich das oben beschriebene Berechnungsverfahren verinnerlichen, wird rasch klar, dass Sie mit dem Inverse Distance Weighting auch eine Voronoi-Zerlegung Ihres Gebietes vornehmen können.
Diese wird natürlich unter Verwendung dieses Tools nach wie vor in 2D- oder 3D-Rasterformate geschrieben. Setzen Sie dazu einfach die Anzahl der zu verwendenden Punkte (max. point number) auf 1. Dann wird zu jedem Interpolationspunkt immer nur der nächstgelegene Eingabewert für den Interpolationspunkt herangezogen, wodurch keine Mittelwertberechung mehr stattfindet, da das Gewicht dieses Punktes auf sich selbst normiert immer 1 ist. So entsteht automatisch eine Voronoi-Zerlegung. Falls Ihnen der Begriff Voronoi noch nicht bekannt ist, können Sie unter https://en.wikipedia.org/wiki/Voronoi_diagram nachschlagen.
¶ Inverse Distance Weighting IDW
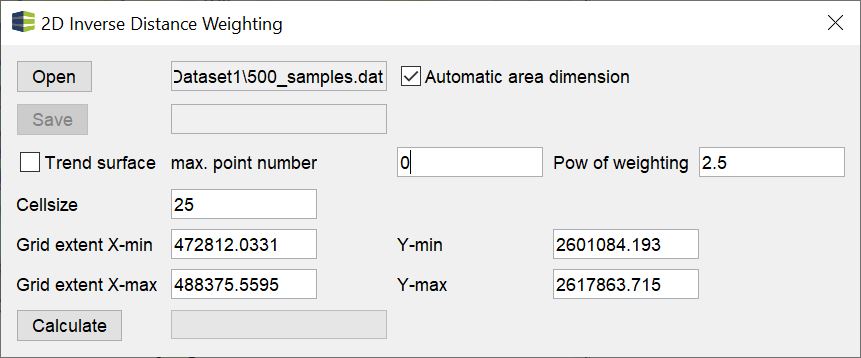
Unter diesem Titel ist im Menü Modelling die Interpolationsmethode für den 2D-Raum zu finden.
Die Handhabe ist sehr einfach gehalten. Sie öffnen einfach mit Open Ihre Daten (Formate). Sobald Sie sie eingeladen haben und das Häkchen bei Automatic area dimension aktiv ist, werden die Textfelder für die Dimension eines Ausgabe-Rasters (Grid) gleich vorgeschlagen. Wenn Sie wissen möchten, welche Ausgabe-Formate Sie von dieser Funktion erwarten können, dann können Sie hier die Formate für Rasterdaten nachschlagen.
Lesen Sie die Einleitung dieses Artikels um die Textfelder max. point number und Pow of weighting zu verstehen und hier sinnvolle Werte einzugeben. Standardmäßig ist max. point number auf 0 eingestellt, das heißt alle Eingabewerte fließen in die Berechnung eines Interpolationspunktes. Pow of weighting schlägt standardmäßig einen Wert von 2.5 vor. Wir empfehlen jedoch mehrere Berechnungen mit Variationen des Exponenten zu rechnen und die Ergebnisse auf Plausibilität zu bewerten.
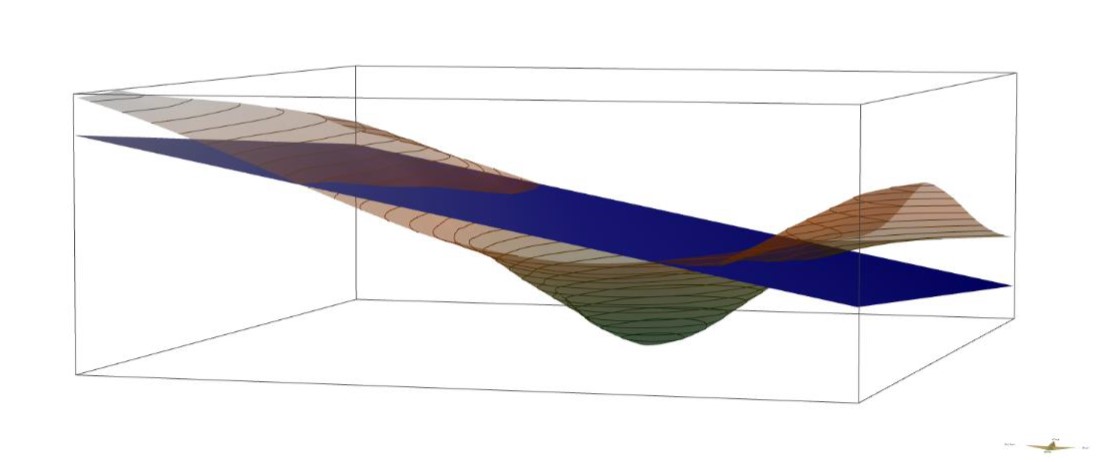
Wenn Sie ein Häkchen bei Trend surface setzen, dann wird vor der Interpolation eine lineare Regression über die Eingabewerte berechnet. Dabei entsteht eine lineare Trendfläche. Anschließend werden die Residuen, also die Abweichungen, der Eingabewerte von der Trendfläche berechnet. Die Residuen werden dann für die Interpolationsberechnung verwendet. Ist diese abgeschlossen, wird der Interpolationswert wieder von der Trendfläche zurück gerechnet. So erhalten Sie eine Interpolation, die nicht durch einen globalen Trend verzerrt ist. Liegt im Gebiet gar kein Trend vor, so wird sich das Ergebnis nur sehr wenig von einem unterscheiden, bei dem Sie keine Trendflächenberechnung gesetzt haben. Bedenken Sie aber, dass bei sehr vielen Eingabewerten, die Regression etwas Berechnungszeit in Anspruch nimmt.
Tipp:
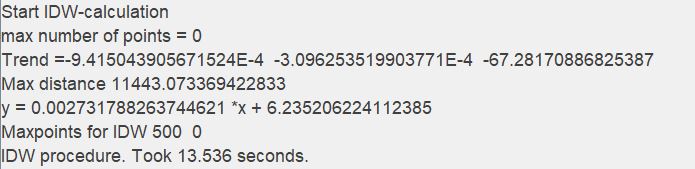
Sie können sich das Berechnungsprotokoll auch im Info-Window anschauen. Dort werden Sie die Parameter der Trendflächenberechnung finden. Bei "Trend=v1 v2 v3" sind die drei Parameter gelistet, die Sie mit v1 * x + v2 * y + v3 berechnen, um den Trendwert an einem bestimmten Standort zu erhalten. Bei "y=..." sehen Sie den Gradienten des linearen Trends, wobei x und y nicht mit den XY Koordinaten zu verwechseln sind. Diese Formel bezieht sich auf die Neigung der Fläche.
In den Beispielen unten haben wir einmal die Ergebnisse verschiedener Berechnungen gegenüber gestellt:
¶ Mit und ohne Trend
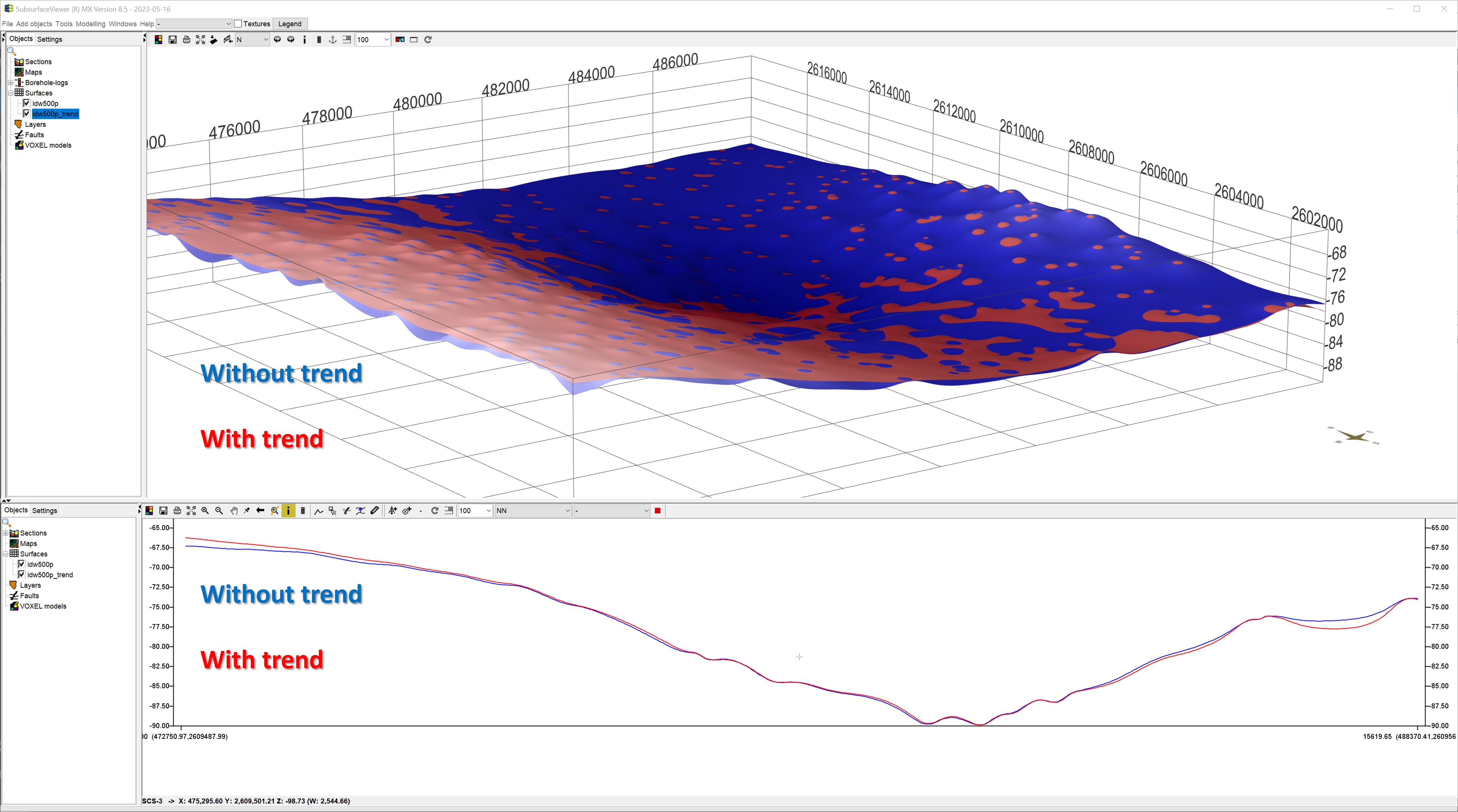
Sie sehen die Gegenüberstellung einer Inverse Distance Interpolation mit und ohne Trendflächenberechnung. Da die Trendfläche in Ihrer Neigung derjenigen im obigen Beispielbild entspricht, können Sie hier nun gut den Effekt des Detrendings vor der Interpolation auf das Ergebnis nachvollziehen.
¶ IDW mit verschiedenen Einstellungen
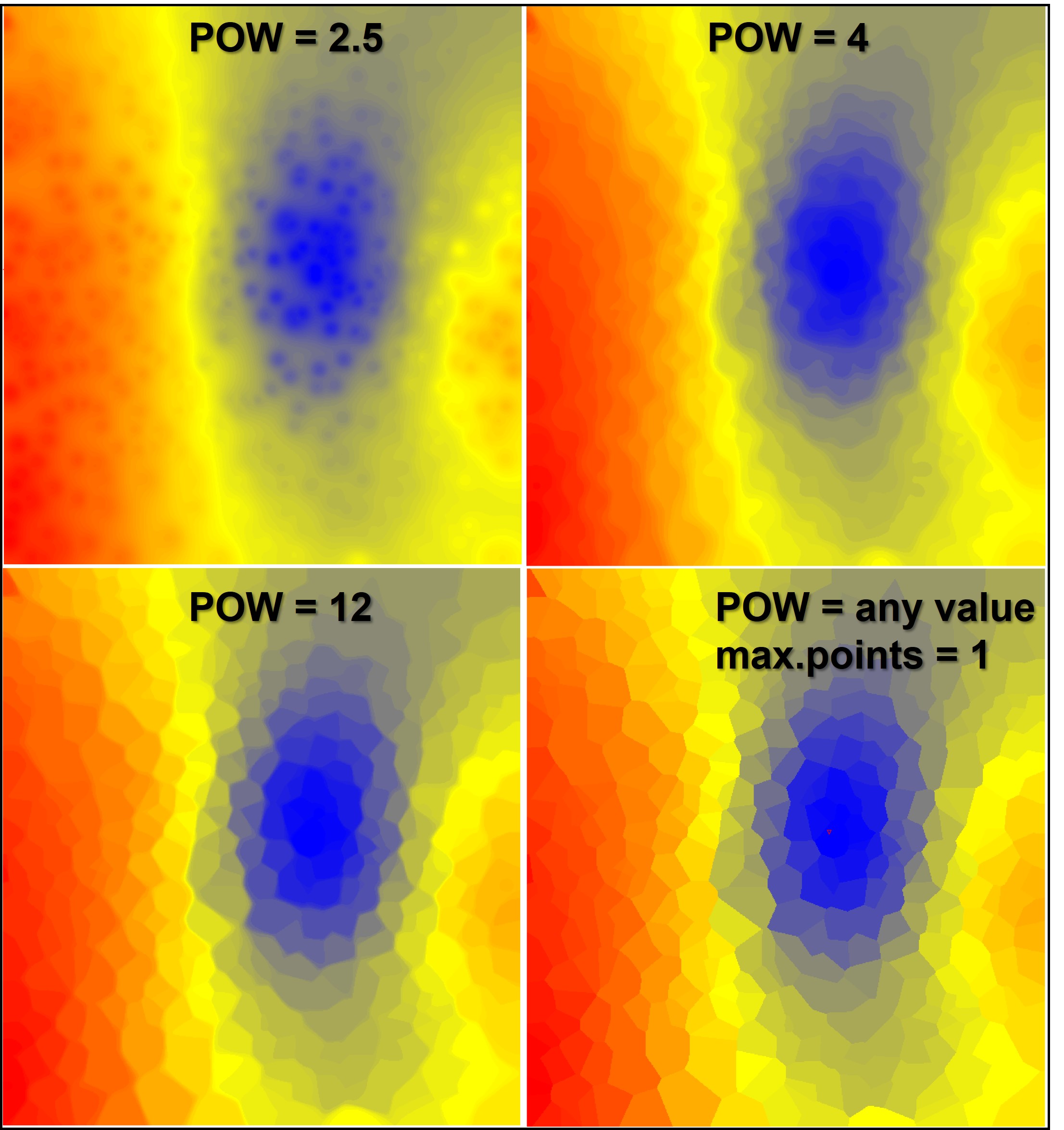
Hier ist eine Gegenüberstellung von IDW-Interpolationen mit verschiedenen Exponenten abgebildet. Die Berechnung unten rechts entspricht der oben beschriebenen Einstellung für eine Voronoi-Zerlegung. Am Bild unten links können Sie sehen, dass auch ein sehr hoher Exponentialwert sich letztlich einer Voronoi-Zerlegung annähert, da die Einflussnahme von Werten schon bei geringen Distanzen stark abnimmt. Probieren Sie also mit Ihren Daten verschiedene Optionen aus. Bedenken Sie auch die Potenzregeln für negative Exponenten und kleiner 1.
¶ 3D Inverse Distance Weighting
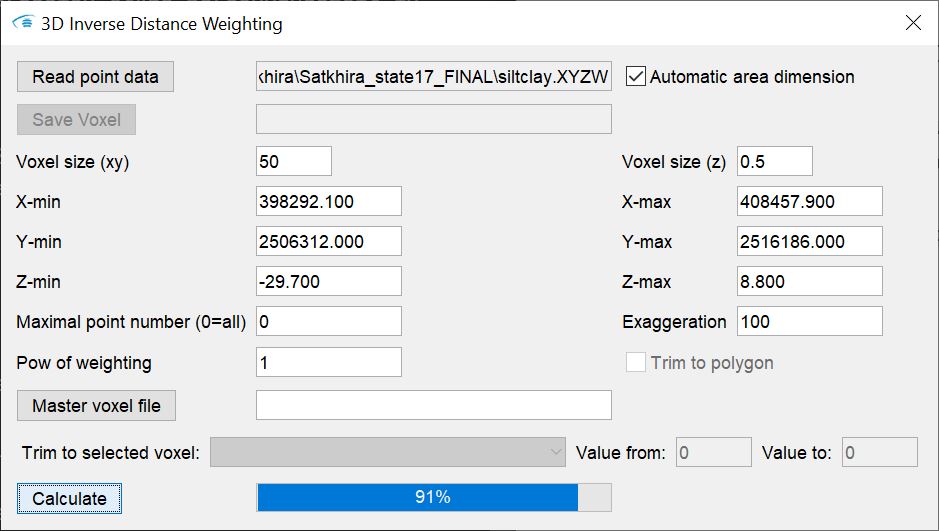
Mit diesem Tool wird die Inverse Distance Weighting Interpolation im 3D-Raum ausgeführt. Das Ausgabeformat ist ein reguläres Voxelmodell (Formate).
Die Theorie bleibt natürlich die Gleiche, wie in der Einleitung beschrieben, und auch der Aufbau der Benutzeroberfläche des Tools ist ganz ähnlich aufgebaut, wie für das 2D-IDW-Tool.
Sie laden mit Read point data die Daten in diesen Formaten ein. Die Dimension der Ausgabe definieren Sie in den Textfeldern darunter. In dem Feld Maximal point number (0=all) geben Sie die Anzahl von Eingabewerten ein, die für eine Interpolation herangezogen werden sollen. Dies entspricht im 2D-IDW dem Feld max. point number. Intensivere Erläuterungen hierzu finden Sie in der Einleitung dieser Seite.
Für die 3D-Interpolation haben Sie dann noch die Möglichkeit mit Exaggeration einen Überhöhungsfaktor einzustellen. Dieser Faktor repräsentiert die in geologischen Ablagerungsräumen übliche vertikal-zu-horizontal-Anisotropie. Sie beeinflusst maßgeblich die Distanzen zwischen den Punkten in der Vertikalen und somit auch die Einflussnahme auf den Interpolationspunkt. In den meisten Fällen - und vor allem, wenn Sie Daten aus Bohrungen interpolieren - ist eine Überhöhung dringend empfohlen. Sie müssen selbst einen geeigneten Faktor durch Versuch und Plausibilitätsprüfung des Ergebnisses wählen.
Der Eintrag Pow of weighting entspricht dem Exponenten, den Sie für die Berechnung wählen müssen. Bitte lesen Sie auch für diese Erläuterung die Einleitung dieses Artikels.
Haben Sie im Projekt ein Polygon, etwa eine Gebietsumrandung, durch copy im Zwischenspeicher hinterlegt, dann ist das Feld Trim to polygon aktiv. Wenn Sie hier ein Häkchen setzen, dann wird nur für Voxel innerhalb des Polygons eine Interpolation durchgeführt. Alle außerhalb liegenden Voxel erhalten einen NoData-Wert.
Sie können aber auch mit Master voxel file ein Voxelmodell laden, welches bereits die Dimension des Ausgabemodells vorgibt und bereits andere Parameter enthält (beispielsweise eine IDW-Interpolation mit anderen Einstellungen).
Wenn Sie die Interpolation nur auf Voxel vornehmen wollen, die zu einem bestimmten Parameter auch nur einen bestimmten Wertebereich aufweisen, dann können Sie die Optionen im Bereich Trim to selected voxel nutzen. Mit der Dropdown-Liste wählen Sie den Parameter aus, auf dem die Bedingung geprüft werden soll. Mit den Feldern Value from und Value to legen Sie einen Wertebereich als Bedingung fest, die erfüllt sein muss, damit die Interpolation stattfindet. Sie können mit dieser Option auch schichtinterne Interpolationen durchführen. Eine ausführliche Anleitung hierzu erhalten Sie unter schichtinterne Parameter-Interpolation.
¶ 3D-IDW mit und ohne Überhöhung
Unten haben wir eine Gegenüberstellung der IDW-Interpolation mit und ohne Überhöhung für Daten aus Bohrungen dargestellt. Die blauen Pfeile sollen Ihnen helfen, leichter markante Unterschiede zu erkennen. Die Daten repräsentieren den Feinkornanteil von Siebanalysen aus Bohrungsmaterial im Modellgebiet Satkhira, welches uns freundlicherweise durch das GSB (Geological Survey Bangladesh) und der BGR (Bundesanstalt für Geologie und Rohstoffe) zur Verfügung gestellt wurde. Bitte beachten Sie, dass das lediglich ein Schaubeispiel ist, und diese Form der Interpolation keine sinnvolle Vorgehensweise zur Handhabe dieser Daten darstellt.
Wird keine Überhöhung eingestellt, so sind die Daten, die aus derselben Bohrung stammen, grundsätzlich mit näheren Distanzen so stark einflussnehmend, dass Daten aus einer weiter entfernt liegenden Bohrung wesentlich geringere Gewichte erhalten. Das bewirkt, dass sich in der Vertikalen des Voxelmodells logischerweise auch wenig Variation ergibt, weil die Bohrungen sozusagen "im Ganzen" auf den Interpolationspunkt Einfluss nehmen. Mit einer Überhöhung sieht das Ergebnis schon etwas plausibler aus.
| Ohne Überhöhung | Mit Überhöhung (100) |
|---|---|
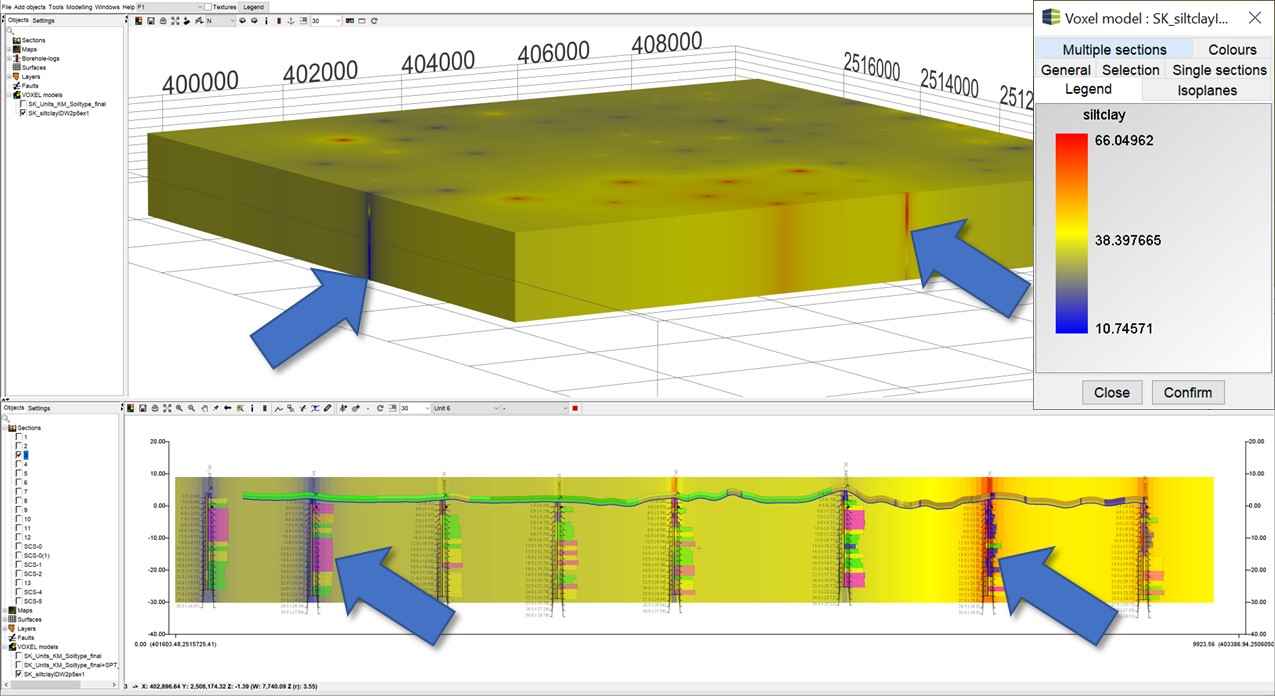 |
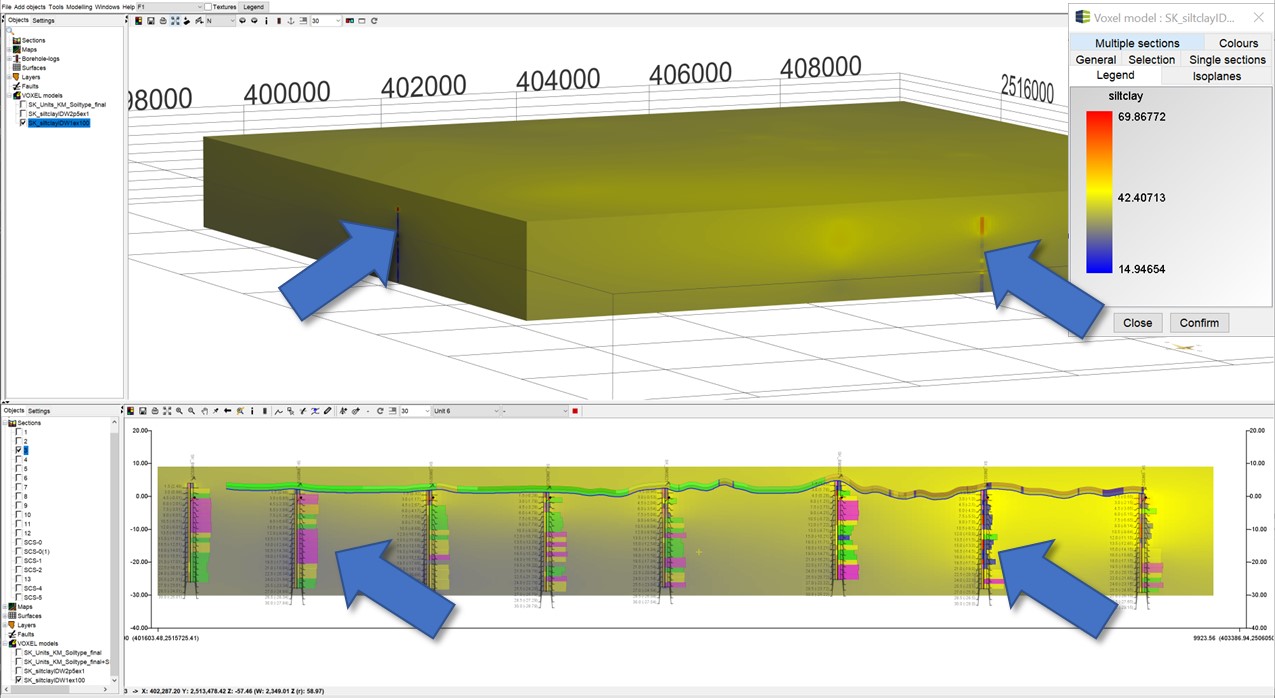 |