Hinweis:
Der SubsurfaceViewer bietet 2D- und 3D-Punkt-Kriging zur Interpolation von Parametern für geologische Schichtenmodelle für Lockersedimente an. Die Implementierung erfolgte projektspezifisch und wurde an die Bedürfnisse der Anwender angepasst, so dass Sie hier ein bewusst leicht verständliches Werkzeug für Kriging in bestimmten Fragestellungen auffinden werden.Die Anwendung deckt jedoch nicht die gesamte Breite möglicher Kriging-Methoden und -optionen ab. Sollten Sie dies benötigen, wird empfohlen ein auf Kriging spezialisiertes Programm zu bevorzugen.
Sie können uns auch gerne kontaktieren, wenn Sie das Gefühl haben, dass wir dieses Thema in unseren weiteren Entwicklungen für Sie ausbauen sollten. Kommen Sie dazu einfach mit uns ins Gespräch.
Sie finden die 2D- und 3D-Kriging Option in der Hauptmenüleiste unter dem Punkt Modelling.
Alle Kriging-Berechungen im SubsurfaceViewer verwenden die Ordinary Kriging-Methode. Sie haben die Möglichkeit mit verschiedenen Variogrammodellen sowie Schachtelvariogrammen zu arbeiten, einige Einstellungen zur Anpassung des experimentellen Variograms vorzunehmen, die Daten auf Ihre deskriptive Statistik zu prüfen, Kriging mit Anisotropie durchzuführen, und Daten vorab etwas zu transformieren. Mit der Kreuzvalidierung (Cross validation) haben Sie die Möglichkeit die Güte Ihrer Schätzung zu überprüfen.
Wir stellen auch Indikatorkriging für Sie bereit, was sowohl als Grenzwertbetrachtung oder als kategoriales Indikatorkriging verwendet werden kann. Sie können ebenfalls Median Indikator Kriging für die Grenzwertbetrachtung durchführen.
Bitte beachten Sie, dass wir im Rahmen dieses Wiki nicht die Kriging-Theorie abhandeln. Wir zeigen hier lediglich Schaubeispiele, die nicht unbedingt eine sinnvolle Handhabe für die dargestellten Eingangsdaten repräsentieren. Die Beispiele dienen nur der Erläuterung der Funktionalitäten. Auch sprechen wir hiermit keine Empfehlungen für bestimmte Kriging-Einstellungen oder Vorgehensweisen für die Variogrammodell-Anpassung aus. Das ist sehr abhängig von Datensatz, räumlicher Komplexität, räumlicher Verteilung und Werte-Verteilung der Parameter. Es ist nicht unüblich, dass die richtige Nutzung von Kriging etwas Übung und Erfahrung bedarf. Glücklicherweise können Sie jedoch per Internet-Recherche inzwischen relativ viel über dieses Thema erfahren. Möchten Sie tiefer einsteigen und sich zum Thema Geostatistik professionalisieren, können wir Ihnen die Seite von Prof. Michael Pyrcz empfehlen, wo Sie sehr viel Wissen über das gesamte Spektrum der Geostatistik erhalten können. Von hier aus können Sie sich auch nach spezifizierten Anwendungen oder Python-Bibliotheken umschauen, wenn Sie über die Möglichkeiten des SubsurfaceViewers hinaus arbeiten wollen.
Die Kriging-Funktionalitäten des SubsurfaceViewer eignen sich hingegen gut, wenn Sie einfaches Ordinary Kriging oder Indikator Ordinary Kriging im Lockersedimentbereich machen wollen, um erste Abschätzungen zu erhalten, wie bestimmte Parameter verteilt sind. Gibt Ihnen die Kreuzvalidierung gute Ergebnisse zurück, können Sie dieses Kriging auch für weitergehende Untersuchungen nutzen. Die Interaktivität bei der Variogrammerstellung spart Zeit und ist leicht verständlich. Die volle Auswertemöglichkeit Ihrer Ergebnis-Raster mit dem SubsurfaceViewer ist ein weiterer Vorteil.
Öffnen Sie also unseren Menüpunkt zum Kriging, erscheint das unten gezeigte Fenster. Auf der linken Seite können Sie die Daten laden und Einstellungen zum experimentellen (Semi-)Variogram sowie zum Variogrammmodell vornehmen. Hier starten Sie auch die Kriging-Berechnung und die Kreuzvalidierung. Weiter unten links finden Sie Visualisierungen und Optionen zur deskriptiven Statistik. Zentral befindet sich das experimentelle Variogramm sowie das Variogrammmodell in einem interaktiven Zeichnen-Feld. Ganz unten werden Sie mit verschiedenen Reitern die erweiterten Einstellungen zur Variographie und Kriging finden.
Tipp:
Während der Variographie und des Kriging-Prozesses werden viele Protokolle und Informationen ins Info-Fenster geschrieben. Es wird empfohlen dieses einzusehen, um die Güte Ihrer Schätzungen besser überprüfen zu können.
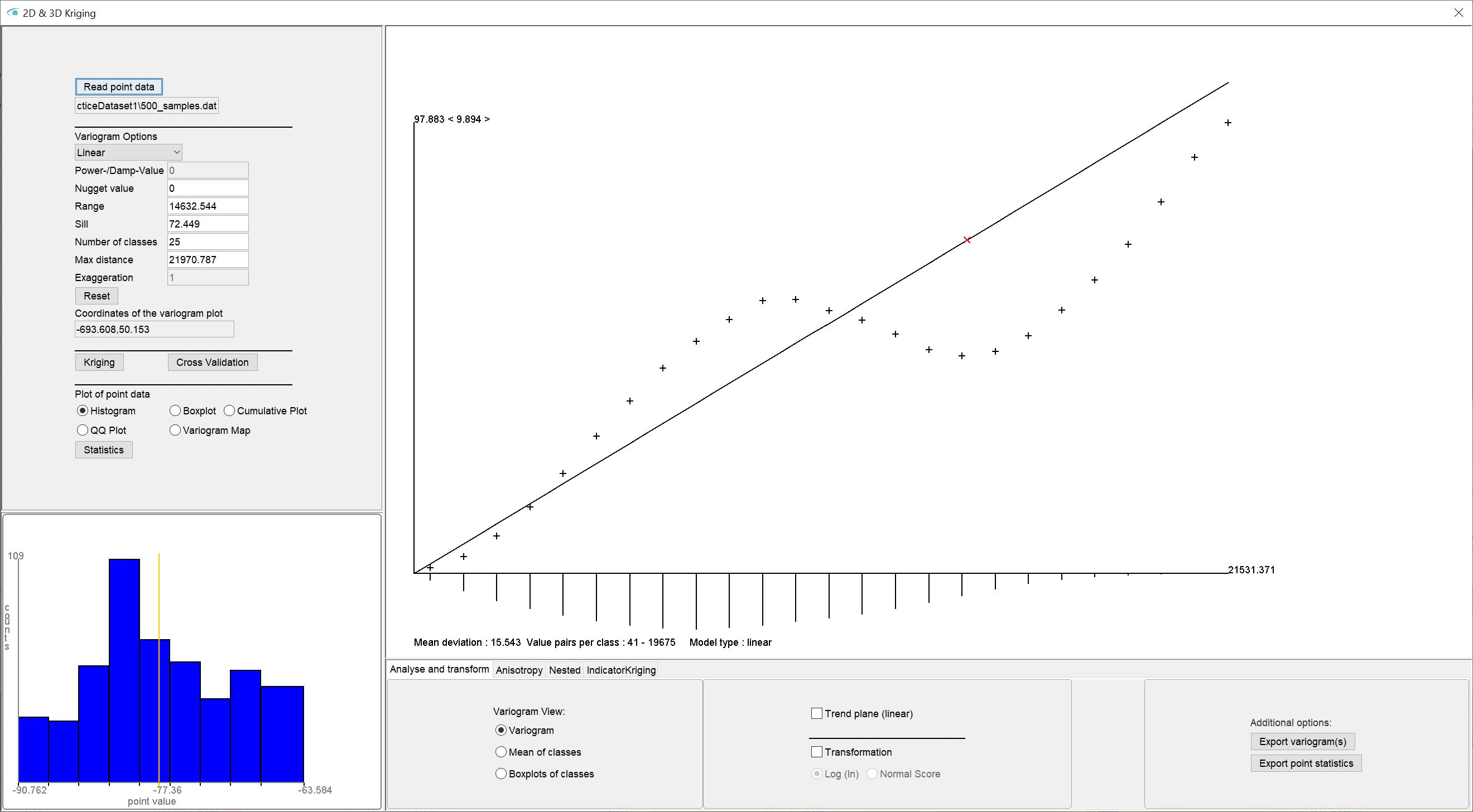
Mit Read Point data laden Sie Ihren Punktdatensatz ein. Die Eingabeformate finden Sie hier. Sobald das Einlesen abgeschlossen ist, wird auch schon das experimentelle (Semi-)Variogramm und die deskriptive Statistik berechnet.
Hinweis: Wenn der Datensatz viele tausend Punkte beinhaltet, kann die Berechnung des experimentellen Variogramms einige Minuten dauern. Es empfiehlt sich dann gegebenenfalls die Daten sinnvoll und sorgsam zu reduzieren oder auf eine andere Anwendung zurückzugreifen.
Im Folgenden wird dieser Artikel für 2D und 3D gemeinsam nach Themen der Variogrammerstellung, der Optionen und der finalen Kriging-Berechnung untergliedert:
¶ Experimentelles Variogramm
In der zentralen Zeichnen-Fläche unseres Kriging-Fensters sehen Sie das experimentelle (Semi-)Variogramm. Es wird in der Literatur auch als empirisches Variogramm oder Stichprobenvariogramm bezeichnet.
Die y-Achse repräsentiert dabei die Varianz, die x-Achse ist die Distanz in Meter. Initial sehen Sie das experimentelle Variogramm als Kreuze.
Das experimentelle Variogramm entsteht durch die Berechnung der Varianzen von Wertepaaren, welche, klassifiziert nach Distanzklassen gemittelt, für jede Distanzklasse hier aufgetragen werden.
Die Formel zur Berechnung der Varianzen sieht folgendermaßen aus:
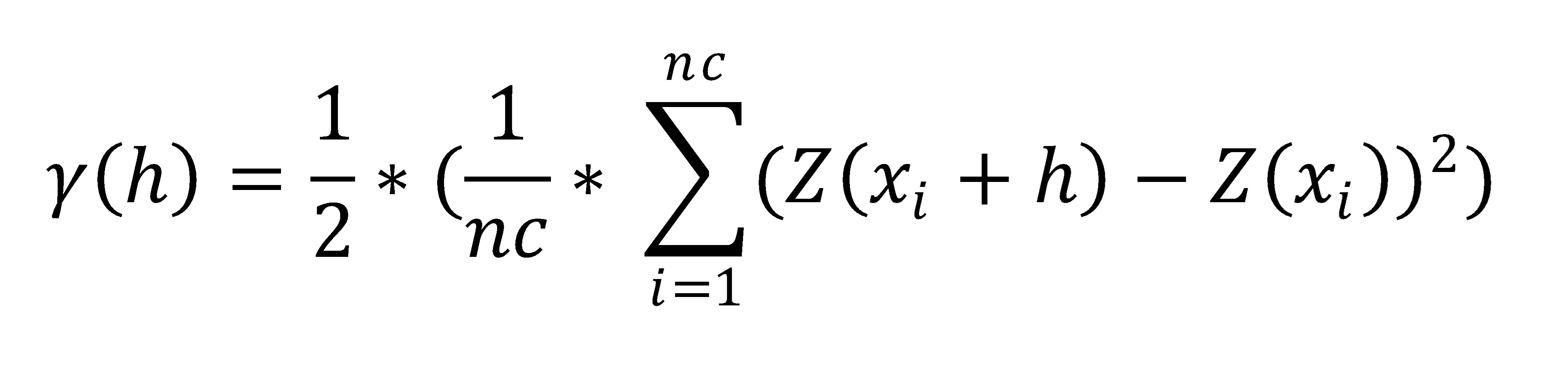
y(h) = Semivarianz für die Distanz(-klasse) h.
nc = Anzahl der Eingabewerte (pro Distanzklasse)
i = Index eines Eingabewertes
Z(xi + h) = Eingabewert am Standort in Distanz h zum Eingabewert an xi
Z(xi) = Eingabewert an xi
Anhand dieser Formel wird schnell klar, dass die finale Teilung des Ergebnisses durch 2, Ursache für den Ausdruck "(Semi-)Varianz" ist.
Der Ablauf der Varianz-Berechnung ist folgendermaßen:
- Die maximale Distanz zwischen den Punkten wird berechnet. Diese kann vom Nutzer unter Max. distance auf der linken Seite auch noch reduziert werden, sofern Bedarf besteht.
- Dieser maximale Distanzwert wird per Angabe der Anzahl für Distanzklassen (Number of classes) unterteilt. Dabei gibt es eine Überschneidung der Klassen immer um die halbe Reichweite der Klasse links und rechts. Bei auf Kriging spezialisierten Programmen, können Sie den Anteil der Überschneidung der Klassen steuern. Das haben wir hier zugunsten einer vereinfachten Handhabe nicht vorgesehen. Erfahrungsgemäß hat sich eine Überschneidung um die halbe Reichweite jedoch häufiger als akzeptabel heraus gestellt.
- Jetzt wird zu jedem Eingabepunkt mit jedem anderen Eingabepunkt die Distanz und die Varianz der Wertepaare berechnet. Entsprechend der Distanz des Wertepaares, wird die Varianz der passenden Distanzklasse zugeordnet. Für das (Semi-)Variogramm in der Standardeinstellung Variogram (im unteren Bereich unter Variogram View) werden die Varianzen, die sich in einer Distanzklasse befinden, gemäß obiger Formel gemittelt. Für die Einstellung Boxplots of classes werden sie für die entsprechende Distanzklasse gesammelt und die Parameter für einen Boxplot (Median, IQR, Ausreißer) berechnet. Diese Ansicht hilft Ihnen die Verteilung der Varianzen in den Distanzklassen besser analysieren zu können. Es kann vorkommen, dass eine Variogrammodell-Anpassung auf den Median einer Varianz-Verteilung vorteilhafter ist, als auf das Varianz-Mittel. Sie sollten dies aber stets mit einer Kreuzvalidierung überprüfen.
- Außerdem wird auch der Mittelwert der in einer Distanzklasse Mean of classes befindlichen Werte ausgegeben.
- Nun werden die Daten im Variogramm dargestellt. Die eingetragenen x-Achsenpositionen entsprechen immer dem mittleren Distanzwert einer Distanzklasse. Auf der y-Achse werden, je nach Einstellung in dem Abschnitt Variogram View im unteren Fensterbereich, der Semi-Varianzwert als Kreuz, der Boxplot mit Median (Strich), Grenzen, Ausreißer und dem Semi-Varianzwert als Kreuz oder der Mittelwert der Eingabewerte in der Klasse als Kreuz dargestellt.
Unten in dem Reiter Analyse and transform haben Sie die Möglichkeit die Ansicht des experimentellen Variogramms interaktiv zu ändern.
Als weitere Hilfestellung zur Bewertung Ihres experimentellen Variogramms wird unter der x-Achse für jede Distanzklasse ein Strich gezeichnet, dessen Länge mit der Anzahl der Wertepaare in der jeweiligen Distanzklasse korreliert. Sie können im Variogramm-Fenster unten links auch eine Angabe Value pairs per class: v1 - v2 finden. Die Werte v1 und v2 ensprechen der minimalen und maximalen Anzahl von Wertepaaren in den erstellten Distanzklassen.
Wichtiger Hinweis:
Wenn Sie mit 3D-Punktdaten ein experimentelles Variogramm erzeugen, dann hat der Überhöhungsfaktor Exaggeration auf der linken Seite im Fenster großen Einfluss auf das Ergebnis. Lesen Sie dazu auch gegebenenfalls den Abschnitt 2D-/3D Inverse Distance Weighting mit und ohne Überhöhung. Mit der Überhöhung wird die vertikal-zu-horizontal-Anisotropie, die in der Geologie üblich ist, berücksichtigt. Sie verändert also die Distanz in der Tiefe und somit auch für diagonal in die Tiefe zueinander liegende Wertepaare. Vor allem, wenn Sie eine Schätzung auf Basis von Bohrungsdaten durchführen wollen, sollten Sie schauen, welche Überhöhung Ihnen Vorteile bei der Variogramm-Erstellung bringt. Da wir für unsere Anwender eine vereinfachte, intuitiv nutzbare 3D-Kriging-Anwendung anbieten wollten, haben wir hier nicht die Kriging-Methode über eine Verrechnung von horizontal und vertikal verschiedenen Variogrammen eingebaut. Wenn Sie das suchen, oder in Raum-Zeit arbeiten, müssen Sie auf eine andere Anwendung zurückgreifen. Für den Lockersedimentbereich im regionalen Maßstab hat sich die vereinfachte Methode bislang als akzeptabel herausgestellt.
¶ Deskriptive Statistik, QQ-Plot und Variogram Map
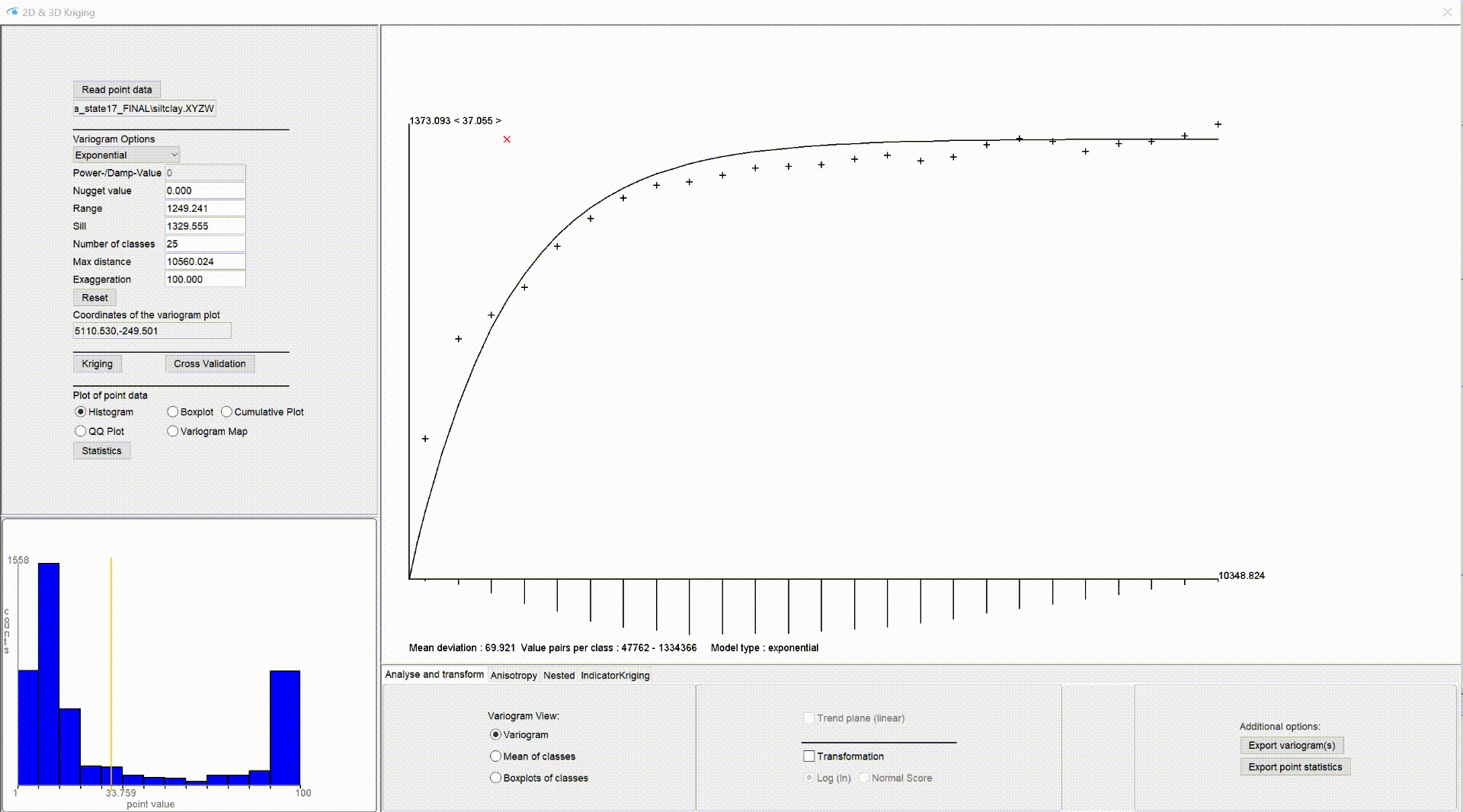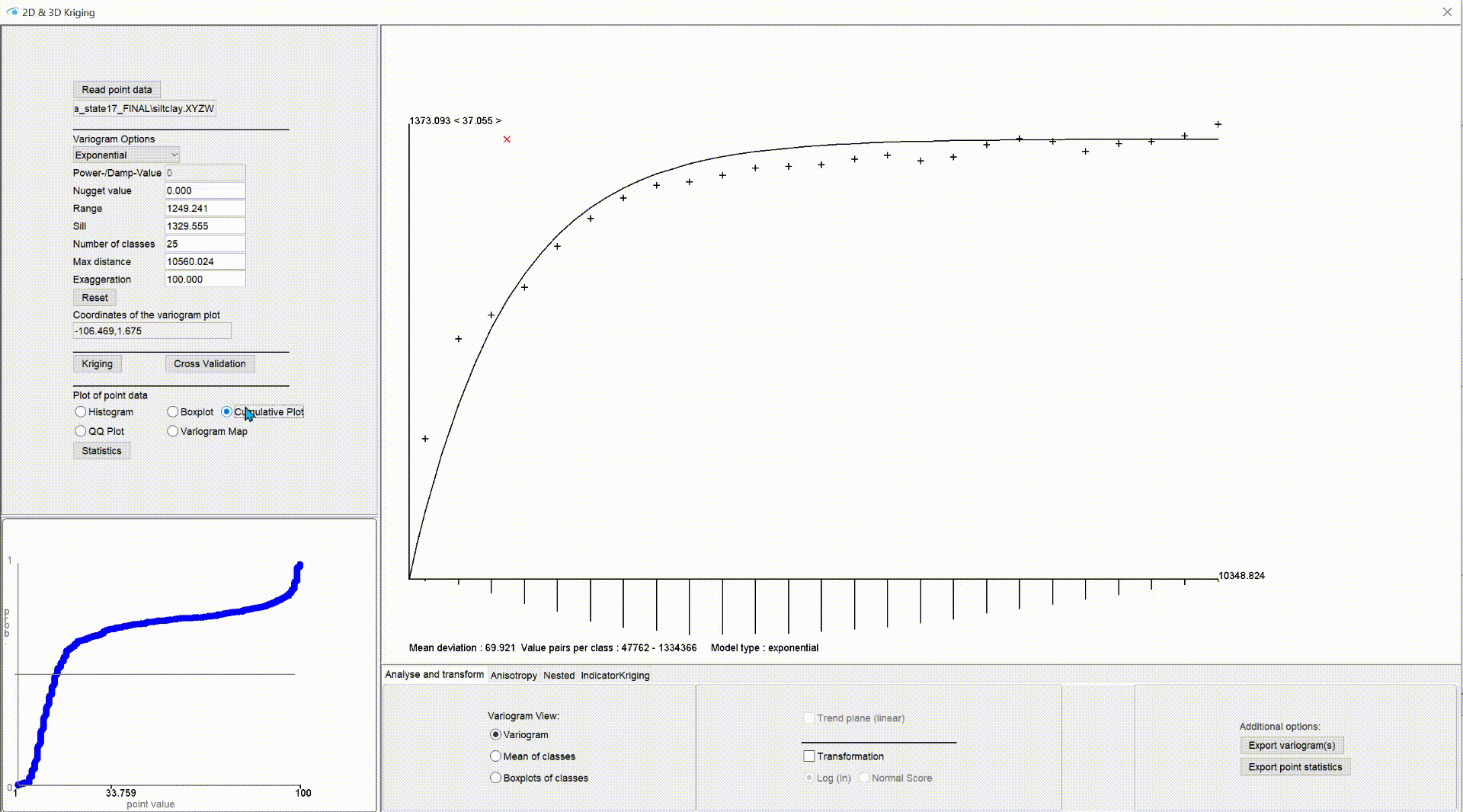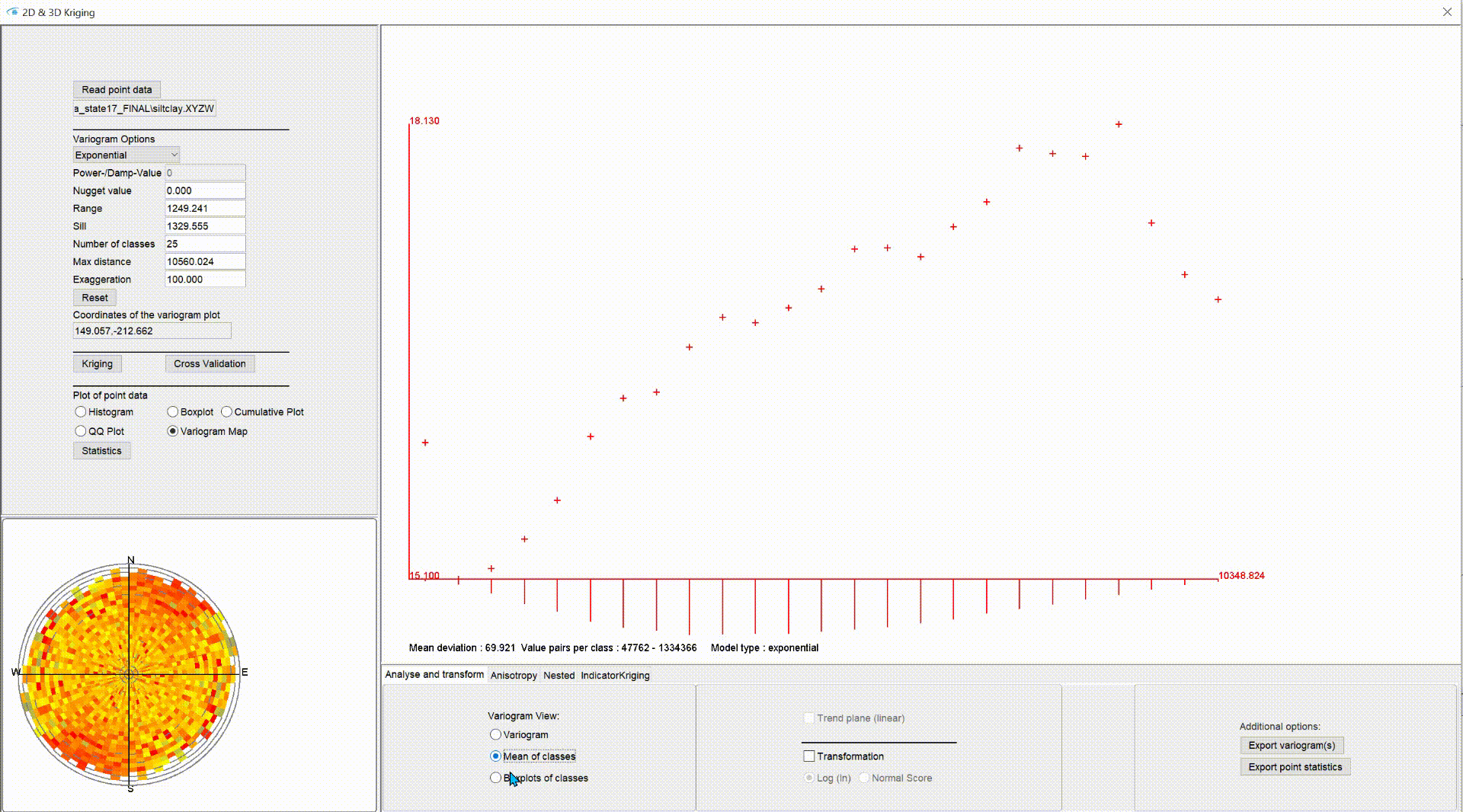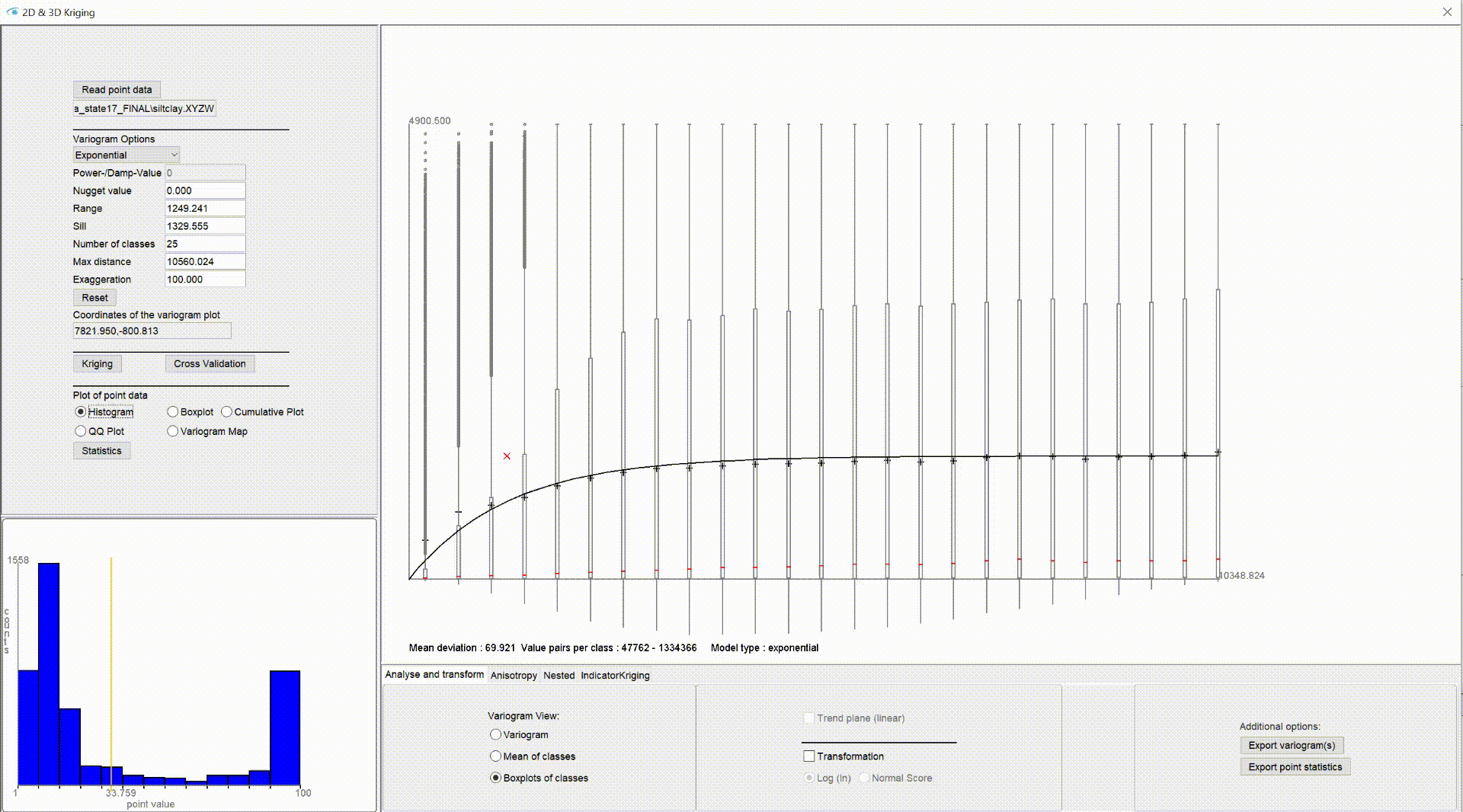
Im linken unteren Bereich unseres Kriging-Fensters sehen Sie eine kleine Graphik, welche, je nach Einstellung, eine Darstellung der deskriptiven Statistik zeigt.
Unter Histogram sehen Sie ein Balkendiagramm über die klassifizierten Wertebereiche mit der Klasseneinteilung der Werte auf der x-Achse und der Anzahl von Werten in einer Klasse auf der y-Achse. Es kann auch großzügig "Histogramm" genannt werden, weil die Klasseneinteilung an jeder Stelle das gleiche Intervall abdeckt - die Klassenbreite ist also überall gleich. Somit korreliert die Anzahl der Werte in einer Klasse mit der relativen Anzahl und kann auf y abgetragen werden. Die Klasseneinteilung wird vereinfacht nach Scott berechnet. Der gelbe vertikale Strich markiert das arithmetische Mittel. Beinhalten die Eingabewerte nur ganze Zahlen und umfassen diese nur ein Spektrum von unter 15 verschiedenen Zahlen, wird die Klassenbreite auf 1 gesetzt, weil wir davon ausgehen, dass dies klassifizierte Daten darstellen könnten. Das ist ein konservativer Ansatz und passt vielleicht nicht zum Charakter aller Daten.
Unter Boxplot sehen Sie den Boxplot zu den Daten. Hier markiert der gelbe horizontale Strich den Median-Wert.
Unter Cumulative Plot sehen Sie auf der x-Achse den Wertebereich und auf der y-Achse aufgetragen die Quantile (0-1, normed cumulative frequency) eines Wertes. Der Plot zeigt nur die Eingabewerte und berechnet keine Kurvenanpassung.
Unter QQ Plot wird der Quantil-Quantil-Plot angezeigt. Dieser dient vereinfacht zur visuellen Überprüfung, ob die Verteilung Ihrer Eingabewerte einer Normalverteilung nahe kommt. Da die Kriging-Schätzung auf gewichteten Mittelwerten basiert (Erklärung weiter unten), gelangen Sie zu plausibleren Ergebnissen, wenn Ihre Daten annähernd normalverteilt sind. Auf der y-Achse sind die empirischen Quantile gegen die theoretischen Quantile der Standard-Normalverteilung aufgetragen. Die blauen Punkte entsprechen also den Quantil-Paaren zu den Eingabewerten. Der grüne Strich markiert die ideale Linie, wenn die empirischen Quantile tatsächlich exakt mit den theoretischen Quantilen übereinstimmen würden. Je weiter also die blauen Punkte von der grünen Linie abweichen, desto weniger ähnelt eine Verteilung auch der Normalverteilung. Beachten Sie, dass der visuelle Test einen statistischen parametrischen Test auf Normalverteilung nicht ersetzen kann. Jedoch haben wir es in der Geologie (Lockersedimente) häufiger mit Daten zu tun, die nicht normalverteilt sind. Es kommt durchaus vor, dass Geologen sich mit einer Annäherung an eine Normalverteilung zufrieden geben und dennoch Kriging durchführen. Diese Entscheidung ist aber sehr abhängig vom Charakter der Eingabewerte, dem Genauigkeitsanspruch der Schätzung, den geologischen Strukturen und letztlich auch der Wertedichte im Gebiet sowie der Gebietsgröße. Beachten Sie auch, dass Ihre Eingabewerte durch eine geclusterte räumliche Verteilung bei gut strukturiertem geologischen Untergrund, an dem der zu schätzende Parameter gebunden ist, auch künstlich schiefe Verteilungen Ihrer Eingabewerte zeigen kann, die eigentlich zugrundeliegende Parameterverteilung dennoch annhähernd normalverteilt wäre. Sie sehen also, dass Kriging in der Praxis ein komplexes Thema werden kann und die Anwendung der Schätzung mit Umsicht erfolgen sollte.
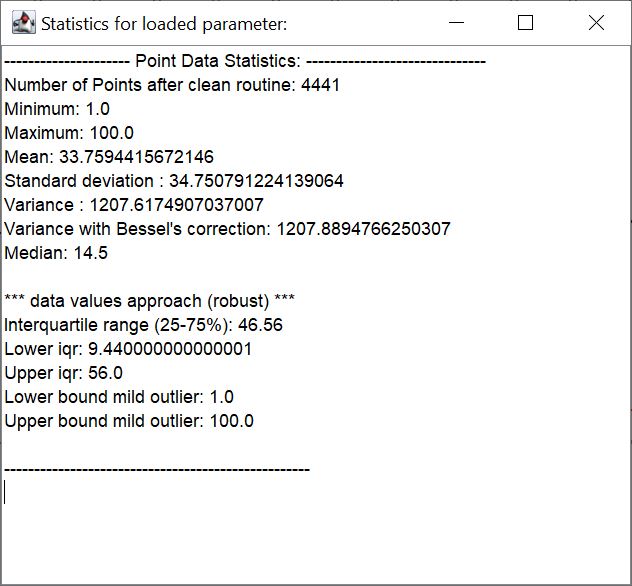
Mit dem Knopf Statistics öffnet sich ein kleines Fenster, mit welchem Sie die Zusammenfassung der deskriptiven Statistik in Textform sehen. Sie können diesen Text dann auch zu Ihrer Dokumentation mit Export point statistics exportieren oder mit copy-paste woanders ablegen.
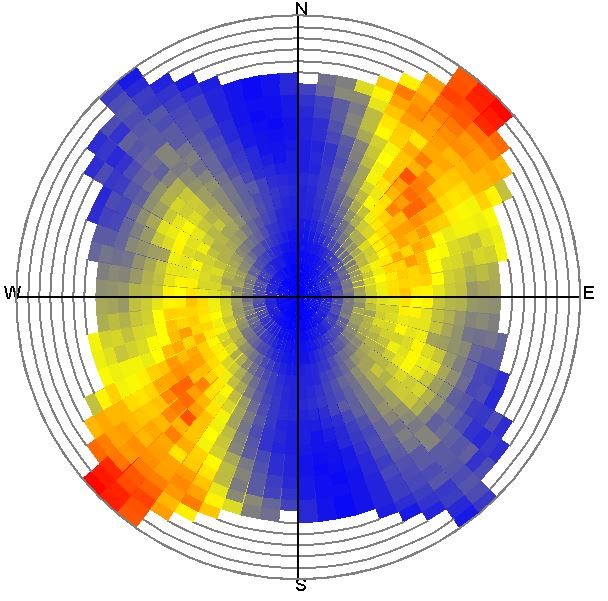
Unter Variogram Map sehen Sie die Variogramm-Karte. Hier werden die Varianzen richtungsabhängig und zu jeder Distanzklasse eingetragen. Die Richtungsklassen werden von Norden im Uhrzeigersinn in 5°-Schritten erstellt. Dann werden die Semi-Varianzen pro kombinierter Richtungs- und Distanzklasse berechnet (siehe hierzu auch oben).
Die Distanzklassen mit geringen Distanzen starten vom Mittelpunkt der Variogram Map. Deren Grenzen werden durch einen grauen Ring repräsentiert. Der Radius des Außenrings entspricht also der Max. distance.
Die Färbung wird immer relativ am Interval der minimalen und maximalen Varianzen bemessen. Blau startet mit dem minimalen Varianzwert, dann folgt Gelb und schließlich endet Rot mit dem maximalen Varianz-Wert, der in den Klassen berechnet wurde.
Mit einer Variogram Map können Sie rasch visuell richtungsabhängige Anisotropien in Ihrem Datensatz entdecken. In der Abbildung hier sehen Sie eine deutlich räumlich strukturierte Verteilung der Parameter-Varianz. Anders ist dies in dem Beispiel weiter oben. Dort zeigt die Variogramm-Karte eher eine zufällig fluktuierende räumliche Verteilung der Varianz - also keine Anisotropie.
Die Variogram Map wird einmal erstellt, sobald Sie zu dem aktuellen experimentellen Variogramm auf den Button Variogram Map drücken. Bei einem großen Datensatz (mehrere tausend Punkte) kann die Erstellung der Variogram Map einige Zeit dauern. Es bleibt aber dann dieselbe Variogramm-Karte (kostet also keine Zeit mehr), solange Sie nicht durch Änderungen entsprechender Einstellungen ein neues experimentelles Variogramm berechnen. Dann muss auch die Variogramm-Karte neu berechnet werden.
¶ Transformationen der Daten
Sie können Ihre Daten auch transformieren, wenn Sie erreichen wollen, dass sich die Verteilung Ihrer Eingabewerte eher einer Normalverteilung ähnelt. Sie finden Funktionen hierzu unten im Fenster im Reiter Analyse and transform und dort dann mittig.
.gif)
Wenn Sie mit 2D-Daten arbeiten, können Sie Trend plane (linear) aktivieren. Es wird dann vor der Variogramm-Berechnung (und auch respektive dem Kriging) eine lineare Regression über die Eingabewerte berechnet. Dabei entsteht eine lineare Trendfläche. Anschließend werden die Residuen, also die Abweichungen, der Eingabewerte von der Trendfläche berechnet. Die Residuen werden für alle weiteren Berechnungen verwendet. Beim Kriging wird der finale Schätzwert wieder von der Trendfläche zurückgerechnet. So erhalten Sie eine Schätzung, die nicht durch einen globalen Trend (externe Drift) verzerrt ist.
Weitere Datentransformationen bieten wir als Log (ln) und Normal score Transformation an. Sie setzen hierzu einfach das Häkchen bei Transformation aktiv und wählen die entsprechende Methode aus. Wenn Ihr Datensatz Werte kleiner gleich 0 enthält, können Sie die Log (ln) Transformation nicht durchführen. Sie erhalten eine Fehlermeldung und es wird keine Transformation auf Ihren Daten durchgeführt. Die Normal score-Transformation macht sich wieder die Quantile der empirischen Werte und der der standardisierten Normalverteilung zunutze. Hier werden also entsprechend dem Quantil des Eingabewertes der Äquivalentwert zum Quantil aus der standardisierten Normalverteilung genommen und für alle weiteren Berechnungen verwendet. I.d.R. ist diese Transformation recht robust. Bei einigen Datensätzen können aber Unstimmigkeiten an den äußeren Rändern der Verteilung entstehen. Hier muss sorgsam eine Entscheidung zur oder gegen eine Nutzung getroffen werden. Sie sollten eine Normal Score Transformation auch nicht unbedingt auf kleinen Datensätzen durchführen. Die Rücktransformation der finalen Schätzwerte in die Verteilung Ihrer Eingabewerte nutzt ausschließlich lineare Methoden.
Bei 2D-Daten können Sie eine Kombination von Trend plane (linear) und Transformation machen. Wir haben im Programm darauf geachtet, dass die Kombination intern immer in der richtigen Reihenfolge stattfindet, so dass Sie sich hierzu keine zusätzlichen Gedanken machen müssen.
Wichtiger Hinweis:
Beim Kriging mit dem SubsurfaceViewer werden mit Methoden der Rücktransformation die Schätzwerte wieder in die Verteilung der Eingabewerte gebracht. Wir haben dies aber nur für die Schätzwerte selbst implementiert, nicht jedoch für die Kriging-Varianz bzw. -Standardabweichung. Diese können Sie bei Verwendung einer Transformation leider nicht für Ihre Auswertung nutzen.
Um Ihre Transformation zu dokumentieren, können Sie die Funktion Export point statistics nutzen, dann wird Ihnen ein Text-Protokoll der deskriptiven Statistik Ihrer Eingabewerte und darunter Ihrer transformierten Werte ausgegeben.
¶ Theoretisches Variogrammodell anpassen
Das theoretische Variogrammodell ist wichtigster Bestandteil der Kriging-Schätzung. Zur Entscheidung und Anpassung eines theoretischen Variogrammodells wird das experimentelle Variogramm überhaupt erst gerechnet. Lesen Sie den Abschnitt Kriging weiter unten, um genau zu verstehen, welche Signifikanz das Variogrammodell für die Kriging-Schätzung hat.
Das zentrale Zeichnen-Feld unseres Kriging-Fensters ist für die Anpassung des theoretischen Variogrammodells interaktiv geschaltet. Sie können dort einfach mit der Maus reinklicken, halten und das theoretische Variogrammodell in die richtige Position ziehen.
Automatisch werden sich dann natürlich die zugehörigen Werte für Sill und Range aktualisieren. Das rote kleine Kreuz im Zeichnen-Feld zeigt Ihnen die Position von Sill und Range in der Graphik an. Der Sill entspricht am roten Kreuz der Position auf der y-Achse. Bei gebundenen Modellen, wie dem sphärischen Modell, ist dieser Wert theoretisch die größte im Gebiet zu erwartene Varianz der Eingabewerte. Der Wert Range entspricht am roten Kreuz der Position auf der x-Achse und ist in Meter zu verstehen. Ab hier ändert sich die theoretische Varianz bei gebundenen Modellen nicht mehr, da keine Autokorrelation mehr vorliegt. Deshalb findet man auch hierzu häufig den Begriff Korrelationslänge. Die Varianz der Daten ist ab dieser Distanz nicht mehr abhängig von der Distanz der Wertepaare zueinander. Bei ungebundenen Modellen, wie dem linearen oder dem exponentiellen Variogrammodell, fließen Sill und Range dichtsdesotrotz in die Berechnungsformeln der Modelle ein, so dass sie stets essentiellen Bestandteil darstellen.
Die Auswahl des Typs des Variogrammodells steuern Sie über die Dropdown-Liste im oberen Abschnitt der linken Optionen-Leiste. Zur Auswahl stehen hier:
- Linear (ungebunden)
- Spherical (gebunden)
- Cubic (gebunden)
- Gaussian (ungebunden)
- Exponential (ungebunden)
- Pentaspherical (gebunden)
- Spherical-Exponential (speziell)
- Hole-effect (speziell)
- Power (ungebunden)
Bitte lesen Sie einschlägige Literatur, um mehr Details und Empfehlungen zu diesen Variogrammodellen zu erhalten. Dies können wir im Rahmen dieses Wiki nicht vertiefen. Wenn Sie einen nicht allzu großen Datensatz haben, können Sie aber auch erstmal intuitiv verschiedene Variogrammodelle anpassen und mit Kreuzvalidierungen und Ergebnis-Checks testen, welches Modell zu der für Sie günstigsten räumlichen Verteilung Ihres Parameters führt.
Der Wert, den Sie unter Nugget value eingeben, ist ein weiterer sehr wichtiger Eingabewert für das Variogrammodell. Der Nugget-Wert bestimmt die in-situ-Varianz, also der natürlichen Varianz, die an Ort und Stelle vorliegt. Das kann aber auch Messfehler beinhalten. In vielen Fällen ist sie 0. Für die Kriging-Schätzung bedeutet dies, dass exakt an der Stelle des Eingabewertes auch der Eingabewert wieder geschätzt wird, so dass man von Erwartungstreue spricht. Ist beim Nugget ein Wert gesetzt, wird einerseits das Variogrammodell bei Distanz 0 auf der y-Achse nach oben, also Varianz != 0 = nugget, verschoben und andererseits bekommen naheliegende Eingabewerte Einfluss auf den Schätzwert an exakt der Stelle des eigentlichen Eingabewertes. Wenn Sie den Abschnitt Kriging lesen, wird Ihnen das vielleicht klarer.
Die Parameter Sill, Range und Nugget fließen also in die Berechnungsformeln der Variogrammodelle direkt ein. Das Hole-effect Modell und das Power-Modell haben als einzige noch einen weiteren Berechnungsparameter. Wenn Sie eines dieser Modelle wählen, dann wird das obere Eingabefeld Power-/Damp-Value aktiv. Haben Sie das Hole-effect Modell gewählt, entspricht der Wert der Distanz (in Meter) ab der die Fluktuation des Hole-effects abgedämpft wird. Ist das Power Modell ausgewählt, entspricht der Wert dem Power-Faktor des Modells. Bei allen anderen Modellen ist das Feld inaktiv.
Das Feld Coordinates of the variogram plot zeigt die Variogramm-Koordinaten bei Ihrer Mausbewegung im zentralen Grafik-Feld und unterstützt Sie bei der Anpassung.
Wenn Sie die entsprechenden Modell-Werte händisch konkret eingeben wollen, weil Ihnen die Werte vielleicht bereits bekannt sind, dann können Sie die Zahlen auch in die entsprechenden Textfelder eingeben. Sobald Sie Ihre Eingabe mit ENTER bestätigt haben, wird das Modell aktualisiert dargestellt.
Unten im Bild des Variogramms sehen Sie auch den Wert Mean deviation, der sich ändert sobald Sie das Variogrammodell ändern. Er entspricht der mittleren Abweichung Ihres Modells von den Semi-Varianzen Ihres experimentellen Variograms. Es ist vorteilhaft eine Minimierung dieses Wertes anzustreben. Eine wirkliche Qualitätsprüfung Ihrer Anpassung sollte letztlich aber mit einer Kreuzvalidierung abgeschlossen werden.
Um eine Variogrammodell-Anpassung zu dokumentieren, haben wir den Export eines einfachen Text-Protokolls eingebaut. Sie finden die Funktion unter Export variogram(s).
Für die speziellen Fälle einer Variogrammodell-Definition im anisotropen Fall und bei Nutzung von Schachtelvariogrammen lesen Sie die entsprechend verlinkten Abschnitte.
¶ Anisotropy
Sie haben die Möglichkeit Variographie mit Anisotropie vorzunehmen. Dazu gehen Sie einfach im unteren Optionen-Bereich unseres Kriging-Fenstes in die Registerkarte Anisotropy und aktivieren das Häkchen bei Directional. Sofort werden die Optionsfelder in der Registerkarte aktiv und zwei experimentelle Variogramme werden berechnet – eines für alle Wertepaare, die die Suchbedingung in Anisotropie-Richtung erfüllen, und eines senkrecht zur Anisotropie-Richtung bzw. außerhalb der Suchbedingung.
Die Suchbedingung setzt sich aus dem Richtungswinkel der Anisotropie Direction of variogram in Grad von Norden (=0°) im Uhrzeigersinn (sowie respektive 180° dazu gespiegelt), dem Öffnungswinkel der Suche, welche Sie mit Angle tolerance einstellen können, und der Bandbreite Bandwidth zusammen. Sie schieben dazu einfach die entsprechenden Regler oder geben eine Zahl in das dazugehörige Textfeld. Sobald Sie ein Feld rechts neben einem Regler mit ENTER bestätigt haben, aktualisiert sich dieser auf die richtige Stelle. Hier müssen Sie für eine Variogramm-Neuberechnung noch einmal auf den „Schiebeknopf“ drücken. Mit Bandwidth stellen Sie die maximale Öffnung der Suchbedingung ein. Auch hier aktualisiert sich die Variogramm-Berechnung mit ENTER.
Das experimentelle Variogramm in Anisotropie-Richtung wird Ihnen in schwarz und das senkrecht dazu in blau dargestellt.
Wenn Sie die Optionen in der Registerkarte Analyse and transform -> Variogram View nutzen, dann erhalten Sie auch hier zwei Graphiken. Schalten Sie auf Mean of classes, dann sind die Werte in Anisotropie-Richtung dunkler rot. Wenn Sie in die Boxplots of classes schalten, dann sind die Boxplots in Anisotropie-Richtung grau und die anderen türkis.
Es empfiehlt sich die Variogram Map links aktiv zu schalten, um einerseits die Anisotropie-Achse in Ihrem Gebiet leichter ausfindig zu machen und andererseits die Variogramm-Anpassung auch mittels der Variogram Map zu optimieren. Beide sind im Falle von aktiven Directional-Optionen in der Darstellung synchronisiert. Sie sehen eine Ellipse (schwarz) und die Reichweite des Öffnungswinkels als graue Schattierung über der Variogram Map. Beides wird sich mit Ihrer Einstellung für die Direction of variogram drehen.
Die Form der Ellipse ist abhängig von den beiden Variogrammodellen, die Sie jeweils einstellen. Wenn Sie ein Variogrammodell ausgewählt haben, wird jeweils eines in blau und eines in schwarz dargestellt. Die Anpassung können Sie entweder auf dem Variogramm in oder senkrecht zur Anisotropie-Richtung vornehmen. Sie schalten dazu einfach zwischen Variogram in anisotropy oder Variogram perpendicular to anisotropy hin und her.
Die beiden Variogrammodelle unterscheiden sich ausschließlich in der Korrelationslänge Range. Der Sill ist stets bei beiden gleich, weshalb sich das schwarze Variogramm ändert, wenn Sie den Sill im Blauen ändern und umgekehrt. Sie werden das rasch merken, wenn Sie die interaktive Anpassung im Fenster vornehmen.
Die Ellipse in der Variogram Map wird sich ändern, wenn Sie die Range-Werte der Modelle ändern. Sie zeigt also die Korrelationslängen in und senkrecht zur Anisotropie-Achse mit ihren beiden Ellipsenachsen. Die finale Ellipse, die durch die verschiedenen Korrelationslängen entsteht, ist ausschlaggebend für die anisotrope Kriging-Schätzung. Der Öffnungswinkel und die Bandbreite hingegen helfen Ihnen nur bei der Erstellung und Interpretation des experimentellen Variogramms.
Wenn Sie mit 3D-Daten reingehen, haben Sie zusätzlich die Möglichkeit die Inklination für die X- und Y-Achse, also die Einfallswinkel, festzulegen. Hierzu nutzen Sie die Regler Inclination (X-Axis) und Inclination (Y-Axis). Diese sind inaktiv, wenn Sie 2D-Daten geladen haben.
Hinweis zur Inklination : Wir haben diese Funktion der Vollständigkeit halber eingeführt, haben aber dazu keine Variogram Map Synchronisation erstellt, da wir uns auf den Lockersedimentbereich konzentrieren und hier eher selten der Einsatz der Inklination notwendig ist. Schreiben Sie uns gerne, wenn Sie denken, dass hier eine Darstellung für Ihre Arbeit unverzichtbar wäre. Vielleicht können wir dies in der zukünftigen Entwicklung berücksichtigen.
Wenn Sie Ihre anisotropen Variogrammodelle finalisiert haben, können Sie zur Dokumentation auch wieder die Funktion Export variogram(s) nutzen. Hier werden beide Modelle dann in einem einfachen Textformat dokumentiert.
¶ Nested variograms
Im unteren Optionenfeld unseres Kriging-Fensters finden Sie den Reiter Nested. Hiermit können Sie Schachtelvariogramme (nested variograms) erstellen. Sie sind eine einfache lineare Kombination aus verschiedenen Variogrammodellen. Die einzelnen Variogrammodelle werden dabei in verschiedenen Farben dargestellt. Das aus der linearen Kombination entstehende finale Variogrammodell ist immer in schwarz gezeichnet. Dies ist das entscheidende Modell für die Kriging-Schätzung.
.gif)
Sobald Sie das Häkchen Nested variograms aktiviert haben, werden zwei Variogrammodelle des zuvor eingestellten Typs erzeugt. Im Feld Number of nested structures sehen Sie also eine 2. Mit mit dem Knopf Add nested structure fügen Sie weitere Variogrammodelle hinzu. Die Anzahl der Strukturen ist unbegrenzt. Die Bearbeitung der einzelnen Modelle schalten Sie über die Dropdown-Liste rechts unter Work with nested nr frei. Ändern Sie jetzt in der Dropdown-Liste für Variogram-Typen oben links den Variogramm-Typ, dann ändert sich dieses und sofort auch das resultierende Variogrammodell.
Das aktive Variogrammodell wird immer etwas dicker gezeichnet als die anderen, so dass Sie es leichter im interaktiven Fenster auffinden. Mit dem Knopf Delete active nested structure können Sie das gerade aktive Variogrammodell wieder löschen.
Sofern Sie nicht die Additive calculation-Funktion aktiv haben, können den verschiedenen Modellen relative Gewichte zugeordnet werden. Hierzu schieben Sie einfach den Regler unter Choose weight of variogram hin und her. Da die Gewichte nochmal im Ganzen normiert werden, kann es sein, dass Sie die Gewichte von allen Variogrammodellen noch einmal ein wenig anpassen müssen, um zu einem guten Ergebnis zu gelangen. Probieren Sie es einfach aus.
Bei der Additive calculation sind die Gewichte unerheblich. Jedes Variogrammodell hat das gleiche Gewicht. Die Modelle werden einfach linear addiert. Das sehen Sie sofort an der Lage des schwarzen Resultat-Modells, wenn Sie die Funktion aktivieren.
Wenn Sie Ihr Schachtelvariogramm finalisiert haben, können Sie zur Dokumentation auch wieder die Funktion Export variogram(s) nutzen. Hier werden alle verwendeten Modelle, ggfls. mit ihren Gewichten, dann in einem einfachen Textformat dokumentiert.
¶ Cross validation
Wenn Sie Ihre Variogrammodell-Definition abgeschlossen haben, können wir empfehlen vor der eigentlichen Kriging-Schätzung eine Kreuzvalidierung zu rechnen. Dies können Sie, indem Sie auf der linken Seite den Button Cross validation betätigen. Es öffnet sich ein sehr einfaches Fenster.
Hier können Sie ein Häkchen bei 10-fold cross-validation setzen, wenn Ihr geladener Datensatz viele tausend Punkte beinhaltet. Ist das Häkchen hier nicht gesetzt, wird eine sogenannte leave-one-out Kreuzvalidierung berechnet. Bei letzterer Methode, wird immer ein Punkt aus dem Datensatz entfernt, die Kriging-Matrix mit den verbleibenden Punkten aufgebaut, und ein Wert genau an der Stelle des ausgelassenen Punktes geschätzt. Dies wird für alle Punkte des Eingangsdatensatzes durchgeführt. Anschließend werden die Abweichungen des echten Datenwertes gegenüber der Schätzung berechnet und in einer Tabelle zusammengefasst. Es wird sich nach Abschluss der Berechnung automatisch ein Fenster zum Speichern dieser Tabelle öffnen.
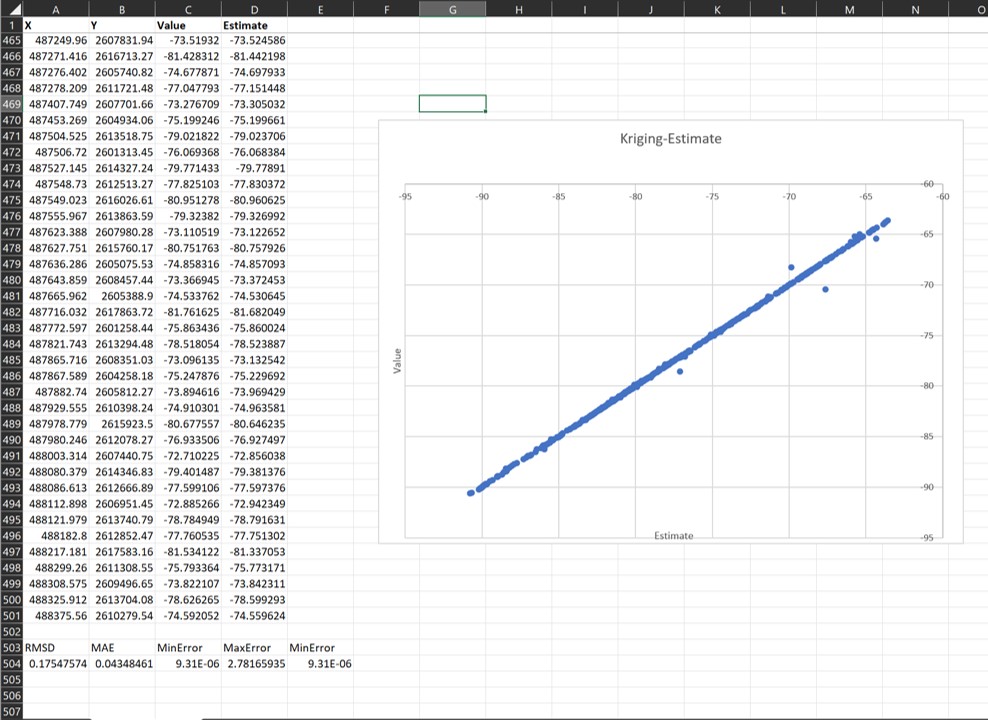
Die Tabelle enthält auch Angaben zur Wurzel der mittleren quadratischen Abweichung (RMSD = root mean square deviation), dem absoluten mittleren Fehler (MAE) und dem minimalen sowie maximalen Fehler, der berechnet wurde. Wenn Sie diese Tabelle mit Excel öffnen, können Sie sich auch einen Graphen erzeugen, der auf der X-Achse die Werte der Eingangsdaten abträgt und auf der Y-Achse den Schätzwert (oder umgekehrt). Streuen die eingetragenen Punkte mehr oder weniger um eine gerade Linie, dem theoretischen Optimum (Schätzwert = originaler Wert, Abweichung = 0), dann könnte Ihre Kriging-Schätzung akzeptabel sein. Letztlich sollten Sie untersuchen, ob Sie mit der Höhe der Abweichungen einverstanden sind.
Wir haben der Tabelle auch die jeweiligen XY-Koordinaten der Punkte beigefügt. Daher können Sie diese Tabelle auch in den Parameter Manager laden, um beispielsweise eine räumliche Ansicht Ihrer Abweichungen zu erhalten.
Wenn Sie eine 10-fold cross-validation durchführen, dann wird im Grunde genauso verfahren, wie es schon oben beschrieben ist, nur dass, anstatt immer ein Wert, 10% des Datensatzes entfernt wird. Diese werden per Zufallsverfahren ausgewählt, jedoch nicht zurückgelegt, so dass gewährleistet ist, dass jeder Punkt einmal Teil des entfernten 10%-Satzes ist.
Hinweis: Wir haben das Tool zur Kreuzvalidierung einfach gehalten, da dies in unseren bisherigen Projekten nicht anders gefordert war. So können Sie leider keine Kreuzvalidierung für den Fall einer Reduktion der genutzten nächsten Punkte (siehe Erklärung hier) zum Aufbau der Kriging-Matrix durchführen. Es werden für die Kreuzvalidierung immer alle Eingangswerte verwendet. Auch die Standardabweichung der Schätzer wird nicht exportiert. Wenn Sie denken, dass wir das in unseren zukünftigen Entwicklungen nachrüsten sollten, schreiben Sie uns gern.
¶ Kriging
Nun möchten Sie nach Ihrer abgeschlossenen Variographie und ggfls. der Kreuzvalidierung die eigentliche Schätzung durchführen? Dann verwenden Sie einfach den Knopf Kriging auf der linken Seite unseres Kriging-Fensters.
Wenn Sie 2D-Daten eingeladen haben, wird die Ausgabe ein Raster sein. Laden Sie 3D-Daten, dann ist die Ausgabe ein reguläres Voxelmodell. Die zur Verfügung stehenden Ausgabeformate können Sie hier nachlesen: für Raster und für Voxelmodelle.
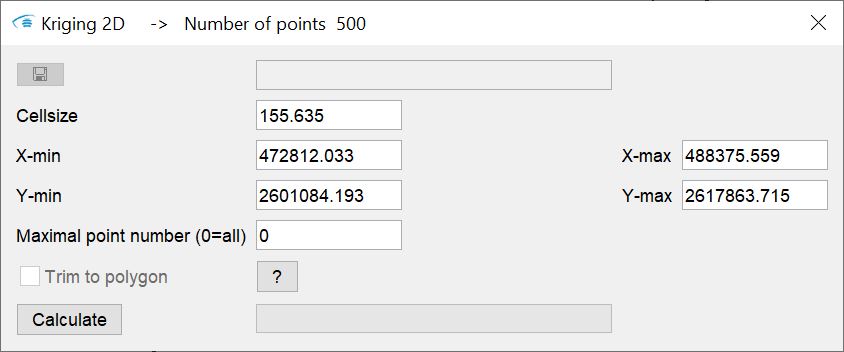
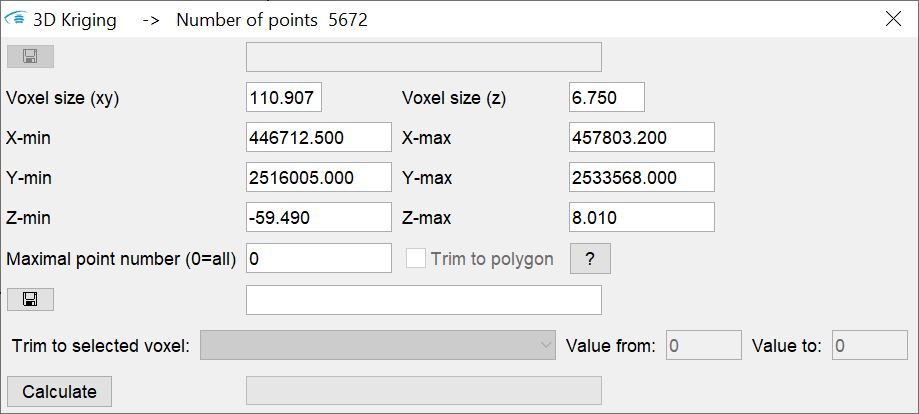
Sie können in dem Fenster die Dimension des Ausgaberasters bzw. des Ausgabevoxelmodells angeben. Haben Sie ein Polygon, etwa eine Gebietsbegrenzung im Zwischenspeicher abgelegt, dann wird das Feld Trim to polyon zur Selektion aktiv. Wenn Sie das Häkchen setzen, findet die Schätzung nur auf Rasterzellen bzw. Voxel statt, die sich innerhalb des Polygons befinden.
Beim 3D-Kriging haben Sie noch die Möglichkeit ein Master als Ausgabevoxel zu laden. Sie laden hierzu einfach ein bereits bestehendes reguläres Voxelmodell. Dieses bestimmt nun die Geometrie der Ausgabe und die Kriging-Ergebnisse werden den bestehenden Voxelparametern einfach hinzugefügt. Wenn Sie nur auf bestimmten Voxeln eine Schätzung durchführen wollen, können Sie das Feld Trim to selected voxel nutzen. Sie suchen mit der Dropdown-Liste denjenigen Parameter aus dem Master-Voxelmodell aus, auf dem Sie filtern möchten. Dann geben Sie rechts ein Werteintervall ein. Nun wird nur noch dort eine Schätzung durchgeführt, wo die Voxel des Master-Modells Werte zu dem selektierten Parameter im angegebenen Werteintervall haben. Sie können diese Funktion auch für ein schichtinternes Kriging nutzen. Wie das geht, haben wir Ihnen in diesem Artikel erklärt.
Dann drücken Sie Calculate, um die Schätzung zu starten.
Der Ablauf des Ordinary-Krigings soll an der Stelle für ein rasches Verständnis kurz erklärt sein:
- Die Kriging-Matrix wird erzeugt. Hierbei werden die Distanzen aller, oder die der maximalen Anzahl von Punkten (Maximal point number (0=all), siehe unten), untereinander berechnet. Auf Basis dieser Distanzen, wird aus dem Variogrammodell die dazugehörige Varianz errechnet. Das ist wichtig, denn Sie haben hier jetzt nicht mehr die experimentelle Varianz vorliegen, jedoch eben die des Variogrammodells.

Verinnerlichen Sie die Ordinary-Kriging-Formel in der Matrix-Schreibweise. y(hi) entspricht dabei immer der Varianz aus dem Variogrammodell für den Distanzwert des Wertepaares, bzw. der Distanz des Wertes zum Schätzpunkt (siehe 2.).
An der Stelle wird Ihnen wahrscheinlich deutlich, welche Relevanz Ihre Wahl und Anpassung des Variogrammodells für die gesamte Schätzung hat. Auf der Diagonalen (von links oben nach rechts unten) steht immer die Varianz des Eingabewertes mit sich selbst. Hier finden Sie also den Wert des Nugget effects. Ist dieser 0, steht in der Diagonalen eben auch überall eine 0. - Die Distanz aller zu verwendenden Eingabewerte zum Schätzpunkt wird berechnet. Gemäß der Distanzen werden wieder Varianzen aus dem Variogrammodell berechnet und diesmal in einen Vektor geschrieben. Sie sehen ihn in der Abbildung der Formel auf der rechten Seite nach dem Gleichheitszeichen.
- Nun fällt Ihnen vielleicht auf, dass in der aufgestellten Gleichung in 1., noch ein Vektor vorhanden ist, der noch nicht erläutert wurde. Das ist der Vektor der Gewichte, die es während des Kriging-Prozesses zu lösen gilt.
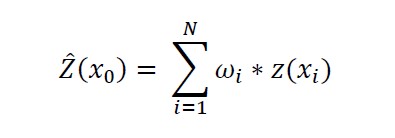
Die Gewichte werden zur Berechnung des gewichteten Mittelwertes der verwendeten Eingangsdaten und der Varianz am Schätzpunkt genutzt. Der gewichtete Mittelwert ist der eigentliche Schätzwert. Die begleitend dazu berechnete Varianz ist die Kriging-Varianz aus der auch die Kriging-Standardabweichung abgeleitet wird.
Zusammenfassend handelt es sich beim Kriging also um die Lösung eines linearen Gleichungssystems.
Um zu gewährleisten, dass die Gewichte in der Summe 1 ergeben, werden die äußeren letzten Glieder der Matrix mit 1 aufgefüllt. Auch im Vektor für die Variogramm-Varianzen am Schätzpunkt wird die letzte Zeile mit 1 besetzt. Das ermöglicht die Lösung des sogenannten Lagrange-Parameters, welcher sich in der letzten Zeile des Gewichte-Vektors befindet. Er kommt auch bei der Berechnung des gewichteten Mittelwertes als Korrekturfaktor zur Verwendung. Zur Lösung des Gleichungssystems muss nun die Kriging-Matrix invertiert werden. Wenn Sie wissen wollen, wie das geht, können Sie online einmal nach den Stichworten „inverse Matrix“ und „Gaußcher Eliminierungsalgorithmus“ suchen. Je nachdem wie viele Punkte Sie für den Aufbau der Kriging-Matrix verwenden müssen, dauert dieser Prozess einige Zeit. - Letztlich werden die geschätzten Werte mit ihrer Standardabweichung (respektive Varianz) in ein vorgegebenes Raster oder Voxelmodell geschrieben und stehen zu Ihrer Analyse bereit.
Beachten Sie, dass der Aufbau einer Kriging-Matrix bei sehr vielen Eingabewerte länger dauern kann. Dauert Sie Ihnen zu lange oder die Matrix wäre zu groß für den Speicher Ihres PCs, dann sollten Sie die Anzahl der Eingabewerte, die zum Aufbau der Kriging-Matrix verwendet werden, reduzieren. Das entsprechende Feld dazu, finden Sie unter Maximal point number (0=all). Setzen Sie hier also eine 0, werden immer alle Eingangswerte verwendet. Ist hier eine Zahl gesetzt, werden die Eingabewerte aufgrund Ihrer Distanz zum Schätzpunkt aufsteigend sortiert. Nur die nächsten Punkte, gemäß der Angabe der maximalen Punkte, fließen in die Kriging-Matrix. Sie müssen hier Ihre Ergebnisse sorgfältig prüfen, besonders dann, wenn Sie einen gut strukturierten Untergrund haben, an dem der zu schätzende Parameter gebunden ist, und gleichzeitig eine eher clusterhafte räumliche Verteilung Ihrer Eingangsdaten vorliegt.
Hinweis: Beachten Sie bei der Reduktion der verwendeten Punkte zum Aufbau der Kriging-Matrix, dass für jeden Schätzpunkt eine eigene Matrix aufgebaut und auch invertiert werden muss. Verwenden Sie alle Eingabepunkte, dann wird die (große) Kriging-Matrix nur einmal aufgebaut, invertiert und für jeden Schätzpunkt wieder verwendet. Unter Umständen kann also eine ungünstige Wahl der maximalen Anzahl der Punkte zu höheren Berechnungszeiten führen als mit der Wahl aller Punkte.
Sobald die Rechnung abgeschlossen ist, wird sich ein Fenster zum Speichern des Ergebnisses öffnen. Im 2D-Kriging werden zwei Rasterdateien erzeugt. In dem einen steht die Schätzung selbst, in dem mit .sdt. gekennzeichneten Raster ist die zugehörige Kriging-Standardabweichung zu finden.
Wenn Sie 3D-Kriging durchgeführt haben, erhalten Sie in Ihrem neu erstellten oder erweiterten Voxelmodell drei neue Spalten. Sie definieren den Namen des Schätzparameters über einen einfachen Eingabedialog, der bei Abschluss der Berechnung und Definition der Datei erscheint. Die Schätzung sowie die zugehörige Kriging-Varianz und Kriging-Standardabweichung werden mit diesem Parameternamen in das Voxelmodell geschrieben.
Wichtiger Hinweis: Sie sollten nach Abschluss der Kriging-Schätzung auch das Info-Fenster sichten. Hier protokollieren wir den Kriging-Prozess. Es werden Hinweise zu ungewöhnlichen Gewichten (Summe der Gewichte ungleich 1) oder ungewöhnlichen Lagrange-Parameter-Werten gegeben. Dadurch erhalten Sie also Hinweise, wie Sie die Güte Ihrer Schätzung einordnen können.
¶ Indicator Kriging
In dem unteren Optionen-Feld unseres Kriging-Fensters finden Sie noch den Reiter Indicator Kriging. Ein Indikator-Kriging kann dann zur Anwendung kommen, wenn Sie…:
- … es mit schief oder multimodal verteilten Parametern zu tun haben,
- … für einen kategorialen Datensatz eine Schätzung durchführen wollen,
- … die Wahrscheinlichkeit schätzen wollen, bei der ein Grenzwert über- bzw. unterschritten wird.
Kurzgefasst schätzen Sie beim kategorialen Indikator-Kriging die Wahrscheinlichkeit des Auftretens einer bestimmten Klasse, dem Indikator bzw. der Kategorie. Oder in anderen Worten, handelt es sich um die Schätzung der relativen Auftrittswahrscheinlichkeit von Werten in einem bestimmten Werteintervall. Die Werte innerhalb der Interquartilsgrenzen beispielsweise haben eine relative Auftrittswahrscheinlichkeit von 0.5, was bedeutet, dass diese Werte in 50% der gemessenen Stichproben auftritt. Wenn wir wieder messen und die Verteilung dieselbe bleibt, dann haben wir wieder eine Chance von 50% Werte innerhalb der Interquartilsgrenzen zu messen. Die Besonderheit des Indikator-Krigings ist natürlich die Betrachtung von Auftrittswahrscheinlichkeiten mit Berücksichtigung der räumlichen Korrelation. Kategoriales Indikator-Kriging können Sie selbstverständlich auch auf den Index-Werten einer bereits vordefinierten Kategorie durchführen, wie etwa der Schicht-ID einer bestimmten geologischen Einheit aus der GVS-Datei. Dann erhalten Sie die relative räumliche Auftrittswahrscheinlichkeit des einen bestimmten Indexes an der Schätzlokation.
Eine weitere Möglichkeit ist die Nutzung von Indikator-Kriging als Grenzwert-Betrachtung. Dann schätzen Sie die relative Wahrscheinlichkeit, ob ein Wert an einem bestimmten Ort unterschritten, respektive überschritten wird. Oder in anderen Worten, handelt es sich um die Schätzung der relativen kumulativen Auftrittswahrscheinlichkeit eines Grenzwertes. Wenn Sie beispielsweise den Wert an der oberen Interquartilsgrenze, also Quartil 75, nehmen, dann ist die kumulative Wahrscheinlichkeit, dass Sie bei einer neuen Messung Werte unterhalb oder gleich dem Quartil 75 messen, 0.75. Sie haben eine 75%ige Chance, dass diese Bedingung erfüllt ist.
Mit dem Button im unteren mittleren Optionen-Feld use as category schalten Sie das kategoriale Indikator-Kriging aktiv. Mit dem Button use as continuous setzen Sie das Grenzwert-Indikatorkriging aktiv. Mit dem Häkchen bei Loaded data is categorical sagen Sie dem System, dass Sie bereits kategoriale Index-Werte als Eingangsdatensatz geladen haben.
Wie Sie es sich aus der vorigen Erläuterung vielleicht schon gedacht haben, können Sie im SubsurfaceViewer sowohl kontinuierliche als auch kategoriale Daten für das Indikator-Kriging laden.
Wenn Sie mit einem kontinuierlichen Datensatz reingehen wollen, können Sie diese Daten intern klassifizieren, bzw. in Grenzwerte einteilen. Sie setzen dazu einfach das Häkchen bei Indicator Kriging auf aktiv. Dann wird bereits auf Basis der robusten deskriptiven Statistik eine Klassifizierung vorgeschlagen. Das erkennen Sie, wenn Sie links das Statistik-Fenster für das Histogram, den Boxplot oder den Cumulative Plot anschauen. Dort sehen Sie nun rote Linien, die die unteren Grenzen der Klassen bzw. die Grenzwerte markieren. Am besten können Sie den Vorschlag nachvollziehen, wenn Sie den Boxplot sichtbar schalten, denn die vorgeschlagene Klasseneinteilung verwendet einfach den Median, die Quartile 25 und 75 sowie das Minimum bei aktivem use as category oder das Maximum bei aktivem use as continuous. Der initiale Vorschlag teilt den Datensatz also erstmal in gleich große Teile auf.
Bei use as category teilen Sie den Datensatz immer mit der unteren Grenze der Klasse/Kategorie. Bei use as continuous teilen Sie mit dem oberen Grenzwert. Bei Loaded data is categorical bildet jeder individuelle Index-Eintrag seine eigene Klasse.
Sie sehen die Klassengrenzen auch im mittleren Bereich der unteren Optionenleiste in dem Textfeld Classification gelistet.
Hinweis: Da Sie für jede Klasse bzw. für jeden Grenzwert-Fall ein eigenes Variogramm definieren müssen, sind die gleichen Werte auch in der Dropdown-Liste unter Define variograms auf der rechten Seite gelistet. Sie schalten mit dieser Liste von einem experimentellen Indikator-Variogramm zum Nächsten.
Wenn Sie eigene Klassen oder Grenzwerte definieren wollen, geben Sie dazu einfach die entsprechenden Unter-/Obergrenzen in das Textfeld Classification ein. Sie sollten dabei das Format des Vorschlags beibehalten – die Werte müssen also Komma-getrennt eingetragen werden. Sobald Sie mit ENTER bestätigen, wird die Dropdown-Liste zum Schalten der entsprechenden Variogramme sowie die roten Linien im Statistik-Plot aktualisiert. Sie können Klassen auch interaktiv im Statistik-Plot definieren. Hierzu doppelklicken Sie einfach an die entsprechende Stelle im Plot und schon wird eine Grenze hinzugefügt, was Sie sowohl im Textfeld als auch in der Dropdown-Liste sehen werden. Mit einem Rechtsklick auf eine rote Linie im Statistik-Plot löschen Sie die Klassengrenze wieder. Zur Orientierung sehen Sie unter dem Textfeld Classification die Koordinaten im Statistik-Plot, wenn Sie sich dort mit der Maus bewegen.
Tipp: Haben Sie einmal eine Änderung vorgenommen und möchten aber wieder zurück zum Klassifizierungsvorschlag, dann deaktivieren Sie das Häkchen bei Indicator Kriging und schalten es danach wieder aktiv. So gelangen Sie wieder zu der Standardeinstellung.
Übrigens: Die Liste der (Klassen-)Grenzwerte ist nach Bestätigung stets von links nach rechts sortiert.
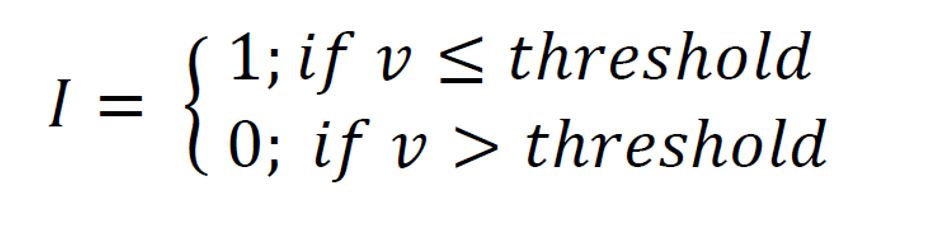
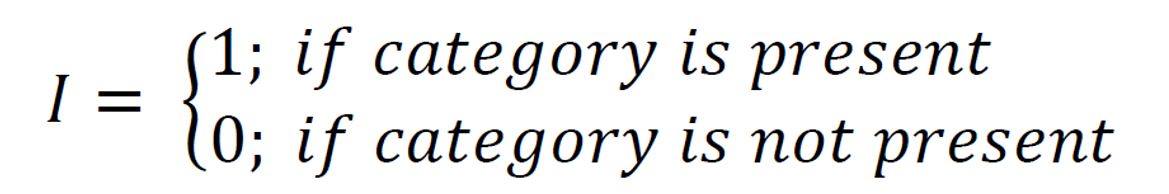
Hier sehen Sie die Formeln für die Indikator-Transformation, die intern stattfindet, sobald Sie eine Klassifizierung oder Grenzwert-Definition bestätigt haben.
Die Indikator-Transformation der Daten beim kategorialen Indikator-Kriging bewirkt im Fall der Erfüllung der Klassenbedingung (Werte liegen innerhalb des Klassenintervalls oder entsprechend genau dem Index der Kategorie), dass an den Lokationen der Eingangsdaten eine 1 gesetzt und in allen anderen Fällen eine 0 wird. Haben wir es mit einer Grenzwert-Betrachtung zu tun, werden überall dort 1en gesetzt, wo die Werte kleiner gleich dem Grenzwert sind, und überall woanders eine 0. Dies wird für jede Klasse bzw. jeden Grenzwert durchgeführt.
Bei 4 Klassen/Grenzwerten haben Sie also auch 4 neue Datensätze im Speicher. Aus diesen 4 neuen Datensätzen werden auch 4 eigenständige experimentelle Variogramme berechnet für die Sie eben auch 4 Variogrammodelle definieren müssen. Wie oben bereits angedeutet, schalten Sie über die Dropdown-Liste unter Define variograms zwischen den Variogrammen zu den intern transformierten Datensätzen hin und her. Die Variogram-Analyse und -Erstellung bleibt wie bekannt und oben beschrieben.
Hinweis: Beachten Sie, dass eine Boxplot-Darstellung der Varianzen für die Distanzklassen hinfällig ist, da die individuellen Varianzen zwischen den Wertepaaren immer nur 1 oder 0 sein können. Damit sind Boxplots nicht darstellbar.
Im Falle der Grenzwert-Betrachtung, haben Sie die Möglichkeit ein Häkchen bei solve via median zu setzen. Es wird Ihnen sofort nur noch ein experimentelles Variogramm gezeigt zu welchem Sie das Modell definieren müssen, nämlich für den Grenzwert Median. Wenn Ihre räumliche Varianz der Auftrittswahrscheinlichkeiten für Ihre gesetzten Grenzwerte immer ähnlich dem des Medians ist, also die experimentellen Variogramme sich sehr ähneln, dann können Sie auch die Kriging-Schätzung nur mit dem zum Median zugehörigen Variogrammodell rechnen. Das spart unter Umständen viel Berechnungszeit, weil die Kriging-Matrix nur anhand des zum Median zugehörigen Datensatzes und Modells aufgebaut wird und dann für jeden Indikator wieder verwendet wird. Diese Methode nennt man auch Median Indicator Kriging.
Hinweis: Haben Sie bei der Grenzwert-Definition den Maximal-Wert aller Eingangswerte in der Dropdown-Liste aktiv und Ihr experimentelles Variogramm zeigt nichts an, wundern Sie sich nicht. Für den Maximal-Wert als Grenzwert ist an allen Lokationen die Grenzwertbedingung erfüllt, da alle Werte kleiner gleich dem Maximum sind. Es wurde also überall eine 1 gesetzt und somit gibt es gar keine Varianz. Dennoch haben wir den Maximal-Wert in unseren Vorschlag hinzugenommen, weil er zur Vervollständigung der theoretisch wieder ableitbaren kumulativen Wahrscheinlichkeitskurve an der Schätzlokation dienen kann. Für den Maximal-Grenzwert wird natürlich auch kein Kriging gerechnet, sondern jede Raster-oder Voxelzelle enthält im Ergebnis für diesen Maximal-Grenzwert einfach eine relative Wahrscheinlichkeit von 1. Das bringt später Vorteile in der Auswertung von Grenzwertbetrachtungen sowie der langfristigen Nachvollziehbarkeit der Schätzung.
Wenn Sie nun, wie gewohnt, das Kriging aktivieren, dann wird für jeden Indikator (Klasse oder Grenzwert) ein Durchlauf mit Ordinary Kriging auf dem entsprechend transformierten Datensatz durchgeführt. Deswegen haben Sie im Fenster zum Starten der Rechnung noch das Häkchen Multi-Threading zur Auswahl. Es werden auf maximal 4 verschiedenen Threads dann die Berechnungen parallel durchgeführt. Alles andere findet genau so statt, wie Sie es in dem Abschnitt Kriging nachlesen können.
In der Ausgabe erhalten Sie dann zu jeder Klasse bzw. zu jedem Grenzwert ein Raster bzw. eine Spalte im Voxelmodell mit der geschätzten relativen Auftrittswahrscheinlichkeit mit Werten zwischen 0 und 1. Die Namen für die Spalten bzw. Rasterdateien werden durch den von Ihnen eingegebenen Parameternamen und dann den betreffenden (Klassen-)Grenzwerten, die Sie während der Variographie festgelegt haben, zusammengesetzt. Haben Sie kategoriales Indikator-Kriging durchgeführt, werden Sie eine zusätzliche Spalte bzw. ein zusätzliches Raster mit dem Zusatz _mostProbable finden. Hier wird an jeder Schätzlokation diejenige Klasse mit der höchsten Auftrittswahrscheinlichkeit mit seiner Klassen-ID in die Rasterzelle bzw. in das Voxel geschrieben.
Wichtiger Hinweis: Sie sollten nach Abschluss der Kriging-Schätzung auch das Info-Fenster sichten. Hier protokollieren wir den Kriging-Prozess. Es werden Hinweise zu ungewöhnlichen Gewichten (Summe der Gewichte ungleich 1) oder ungewöhnlichen Lagrange-Parameter-Werten gegeben. Dadurch erhalten Sie also Hinweise wie Sie die Güte Ihrer Schätzung einordnen können.
Zuletzt sei die Einstellung Simplex method noch erläutert, welche wir Ihnen bis jetzt vorenthalten haben. Sie stellt sicher, dass die geschätzten Auftrittswahrscheinlichkeiten der einzelnen Indikator-Kriging-Läufe im Ergebnis konsistent sind und wieder eine plausible kumulative Wahrscheinlichkeitsfunktion an jedem Schätzstandort theoretisch ableitbar wäre. Die Methode wurde aus der Veröffentlichung Tolosana-Delgado, Pawlowsky-Glahn & Egozcue, 2008: "Indicator Kriging without Order Relation Violations.”, Math Geosci(2008) 40:327-247 entnommen. Der Wert Uncertainty wird dort ebenfalls erläutert. Beachten Sie, dass der Einbau dieser Methode experimentell erfolgte und noch keiner vollständigen Test-Phase unterzogen wurde.
Setzen Sie bei Simplex method kein Häkchen dann wird die Methode, die durch die Funktion ordrel.for aus der inzwischen offen einsehbaren GSLIB-Bibliothek beschrieben wird, mit leichten Anpassungen durchgeführt. Die Korrektur wird, wie die Gewichte und der Lagrange-Parameter im Info-Fenster protokolliert.